
【题目】关于x的方程ax2+bx+c=0(a![]() 0).
0).
(1)已知a,c异号,试说明此方程根的情况.
(2)若该方程的根是x1=-1,x2=3,试求方程a(x+2)2+bx+2b+c=0的根.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第三象限的双曲线
在第三象限的双曲线![]() 上,过点
上,过点![]() 作
作![]() 轴交双曲线于点
轴交双曲线于点![]() ,连接
,连接![]() ,则
,则![]() 的面积为__________.
的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
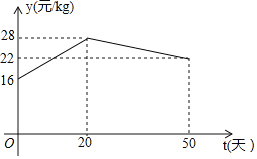
【题目】随着龙虾节的火热举办,某龙虾养殖大户为了发挥技术优势,一次性收购了10000kg小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养10天的总成本为166000,放养30天的总成本为178000元.设这批小龙虾放养t天后的质量为akg,销售单价为y元/kg,根据往年的行情预测,a与t的函数关系为a=![]() ,y与t的函数关系如图所示.
,y与t的函数关系如图所示.
(1)设每天的养殖成本为m元,收购成本为n元,求m与n的值;
(2)求y与t的函数关系式;
(3)如果将这批小龙虾放养t天后一次性出售所得利润为W元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?
(总成本=放养总费用+收购成本;利润=销售总额﹣总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图, 在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结
,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结![]() 交边AB于点
交边AB于点![]() .
.
(1)求AD的长;
(2)设![]() ,
,![]() 的面积为y, 求y关于x的函数解析式,并写出定义域;
的面积为y, 求y关于x的函数解析式,并写出定义域;
(3)过点C作![]() , 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,
, 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,![]() 为等边三角形?请指出点P的位置并加以证明.
为等边三角形?请指出点P的位置并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
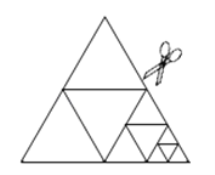
【题目】如图,将一张正三角形纸片剪成四个小正三角形,得到![]() 个小正三角形,称为第一次操作; 然后,将其中的一个正三角形再剪成四个小正三角形,共得到
个小正三角形,称为第一次操作; 然后,将其中的一个正三角形再剪成四个小正三角形,共得到![]() 个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到
个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到![]() 个小正三角形,称为第三次操作;…,根据以上操作,若要得到
个小正三角形,称为第三次操作;…,根据以上操作,若要得到![]() 个小正三角形,则需要操作的次数是__________次.
个小正三角形,则需要操作的次数是__________次.
查看答案和解析>>
科目:初中数学 来源: 题型:
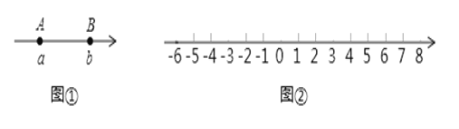
【题目】数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如:如图①,若点![]() 在数轴上分别对应的数为
在数轴上分别对应的数为![]() ,则
,则![]() 的长度可以表示为
的长度可以表示为![]() .
.
请你用以上知识解决问题:
如图②,一个点从数轴上的原点开始,先向左移动![]() 个单位长度到达
个单位长度到达![]() 点,再向右移动
点,再向右移动![]() 个单位长度到达
个单位长度到达![]() 点,然后向右移动
点,然后向右移动![]() 个单位长度到达
个单位长度到达![]() 点.
点.
![]() 请你在图②的数轴上表示出
请你在图②的数轴上表示出![]() 三点的位置.
三点的位置.
![]() 若点
若点![]() 以每秒
以每秒![]() 个单位长度的速度向左移动,同时,点
个单位长度的速度向左移动,同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右移动,设移动时间为
个单位长度的速度向右移动,设移动时间为![]() 秒.
秒.
①当![]() 时,求
时,求![]() 和
和![]() 的长度;
的长度;
②试探究:在移动过程中,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
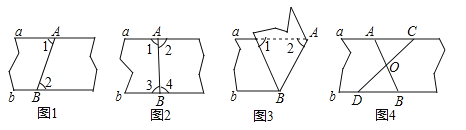
A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠DBA,再添加一个条件,不一定能判定△ABC≌△BAD的是( )
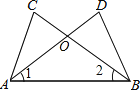
A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com