
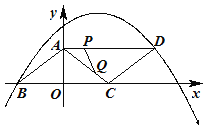
【题目】如图,□ABCD的两个顶点B,D都在抛物线y=![]() x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB=![]() .
.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点E,使以A,C,D,E为顶点的四边形是菱形?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)动点P从点A出发向点D运动,同时动点Q从点C出发向点A运动,运动速度都是每秒1个单位长度,当一个点到达终点时另一个点也停止运动,运动时间为t(秒).当t为何值时,△APQ是直角三角形?
【答案】(1)y=![]() x2+
x2+![]() x+5;(2)存在点E的坐标为(4,6)(3)
x+5;(2)存在点E的坐标为(4,6)(3)![]() 或
或![]() .
.
【解析】试题分析:(1)根据平行四边形的性质,求出A、B、C、D坐标,然后用待定系数法求出函数的解析式;
(2)根据平行四边形的性质和菱形的判定,求出E点的坐标,然后判断其是否在函数的图像上即可;
(3)当△APQ是直角三角形时,分为∠APQ=90°或∠AQP=90°两种情况,通过解直角三角形求解即可.
试题解析:解:(1) ∵OB=OC,OA⊥BC,AB=5,∴AB= AC=5.
∴tan∠ACB=![]() =
=![]() ,∴
,∴![]() .
.
由勾股定理,得OA2+OC2=AC2, ∴(![]() )2+OC2=52,解得OC=±4(负值舍去) .
)2+OC2=52,解得OC=±4(负值舍去) .
∴![]() ,OB=OC=4,AD=BC=8.
,OB=OC=4,AD=BC=8.
∴A(0,3),B(-4,0) ,C(4,0) ,D(8,3) .
∴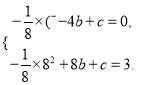
解之得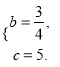
∴抛物线的解析式为y=![]() x2+
x2+![]() x+5.
x+5.
(2)存在.
∵四边形ABCD为平行四边形,∴AC=AB= CD.
又∵AD≠CD,
∴当以A,C,D,E为顶点的四边形是菱形时,AC=CD=DE=AE
由对称性可得,此时点E的坐标为(4,6)
当x=4时,y=![]() x2+
x2+![]() x+5=6,所以点(4,6)在抛物线y=
x+5=6,所以点(4,6)在抛物线y=![]() x2+
x2+![]() x+5上.
x+5上.
∴存在点E的坐标为(4,6)
(3) ∵四边形ABCD为平行四边形,∴AD∥BC,∴∠DAC=∠ACB<90°.
∴当△APQ是直角三角形时,∠APQ=90°或∠AQP=90°.
∵![]() ,∴
,∴![]() .
.
由题意可知AP=t,AQ=5-t,0≤t≤5.
当∠APQ=90°时, ![]() ,∴
,∴![]() ,解得
,解得![]() .
.
当∠AQP=90°时, ![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∵![]() ,
, ![]()
∴![]() 或
或![]() .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】一块直角三角形木板,它的一条直角边AB长1.5m,面积为1.5m2.甲、乙两位木匠分别按图①、②把它加工成一个正方形桌面.请说明哪个正方形面积较大(加工损耗不计).

查看答案和解析>>
科目:初中数学 来源: 题型:
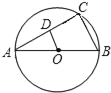
【题目】如图,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sinA﹣1=0,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应国家“自主创业”的号召,某大学毕业生开办了一个装饰品商店,采购了一种今年刚上市的饰品进行了30天的试销,购进价格为20元/件,销售结束后,得知日销售量P(件)与销售时间x(天)之间的关系如图(1)所示,销售价格Q(元/件)与销售时间x(天)之间的关系如图(2)所示.
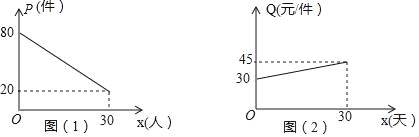
(1)根据图象直接写出:日销售量P(件)与销售时间x(天)之间的函数关系式为 ;销售单价
Q(元/件)与销售时间x(天)的函数关系式为 .(不要求写出自变量的取值范围)
(2)写出该商品的日销售利润W(元)和销售时间x(天)之间的函数关系式;(不要求写出自变量的取值范围)
(3)请问在30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”的进一歩推进,我国瓷器(“china”)更为“一带一路”沿践人民所推崇,一外国商户准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比每个茶杯多120元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)4套茶具的批发价为1280元.
根据以上僖息:
(1)求每个茶壶与每个茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多18个,并且茶壶和茶杯的总数不超过320个,该商户计划将一半的茶具按每套500元成套销售,其余按每个茶壶300元,每个茶杯80元零售.没核商户购进茶壶m个.
①试用含m的关系式表示出该商户计划获取的利润;
②请帮助他设计一种获取利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
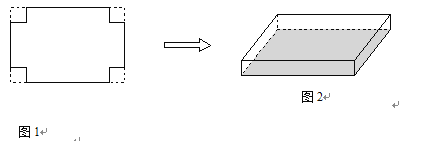
【题目】(本题满分8分)一张长为30cm,宽20cm的矩形纸片,如图1所示,将这张纸片的四个角各剪去一个边长相同的正方形后,把剩余部分折成一个无盖的长方体纸盒,如图1所示,如果折成的长方体纸盒的底面积为264cm2,求剪掉的正方形纸片的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:
我们知道,|m|= .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com