
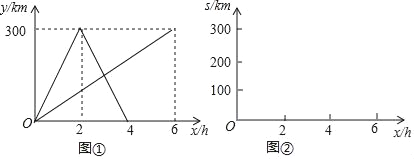
【题目】快车和慢车同时从甲地出发,匀速行驶,快车到达乙地后,原路返回甲地,慢车到达乙地停止.图①表示两车行驶过程中离甲地的路程y(km)与出发时间x(h)的函数图象,请结合图①中的信息,解答下列问题:
(1)快车的速度为 km/h,慢车的速度为 km/h,甲乙两地的距离为 km;
(2)求出发多长时间,两车相距100km;
(3)若两车之间的距离为s km,在图②的直角坐标系中画出s(km)与x(h)的函数图象.
【答案】(1)150,50,300;(2)1 h或2.5h或3.5h;(3)图象见解析.
【解析】分析:(1)观察函数图象可得出甲、乙两地间的距离,根据数量关系速度=路程÷时间即可得出快、慢两车的速度;
(2)根据图象找出点的坐标,利用待定系数法可求出线段解析式,由此即可得出结论;
(3)根据两车相遇结合t=0、2、3、4,6可找出关键点,依此画出函数图象即可.
详解:(1)快车的速度为300÷2=150km/h,慢车的速度为:300÷6=50km/h,甲乙两地的距离为300km,
故答案为:150,50,300;
(2)快车在行驶过程中离A地的路程y1与时间x的函数关系式:
当0≤x<2时,y1=150x,
当2≤x≤4时,y1=300-150(x-2),即y1=600-150x.
慢车在行驶过程中离A地的路程y2与时间x的函数关系式:
当0≤x≤6时,y2=50x,
由题意,得
①当0≤x<2时,y1-y2=100,150x-50x=100,解得x=1;
②当2≤x<3时,y1-y2=100,600-150x-50x=100,解得x=2.5;
③当3≤x<4时,y2-y1=100,50x-(600-150x)=100,解得x=3.5;
④当4≤x≤6时,两车相距大于100km.
答:出发1h或2.5h或3.5h后,两车相距100km;
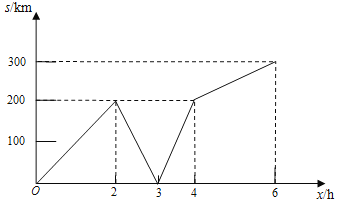
(3)s与x的函数图象如图所示:


科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为50元/件的![]() 恤.经试销发现,销售量
恤.经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数关系,试销数据如下表:
(元/件)符合一次函数关系,试销数据如下表:
售价(元/件) | …… | 55 | 60 | 70 | …… |
销量(件) | …… | 75 | 70 | 60 | …… |
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价![]() 之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种蔬菜![]() 千克,不加工直接出售每千克可卖
千克,不加工直接出售每千克可卖![]() 元;如果经过加工重量减少了20%,价格增加了40%,问:
元;如果经过加工重量减少了20%,价格增加了40%,问:
(1)![]() 千克这种蔬菜加工后可卖多少钱;
千克这种蔬菜加工后可卖多少钱;
(2)如果这种蔬菜1000千克,加工后出售一共可卖2576元,问1000千克这种蔬菜不加工直接出售每千克可卖多少钱?1000千克这种蔬菜加工后出售比不加工直接出售一共多卖多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表:
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人.
(2)求训练后篮球定点投篮人均进球数为多少个?
(3)根据测试资料,参加篮球定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+3(1-k)(其中k为常数,k≠0),k取不同数值时,可得不同直线,请探究这些直线的共同特征.
实践操作
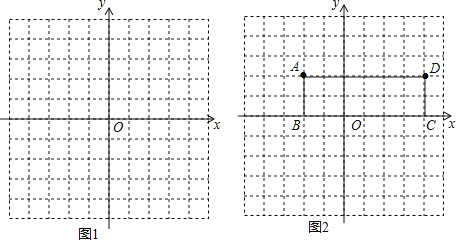
(1)当k=1时,直线l1的解析式为 ,请在图1中画出图象;当k=2时,直线l2的解析式为 ,请在图2中画出图象;
探索发现
(2)直线y=kx+3(1-k)必经过点( , );
类比迁移
(3)矩形ABCD如图2所示,若直线y=kx+k-2(k≠0)分矩形ABCD的面积为相等的两部分,请在图中直接画出这条直线.
查看答案和解析>>
科目:初中数学 来源: 题型:
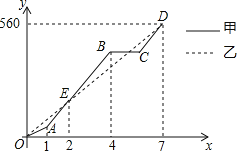
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
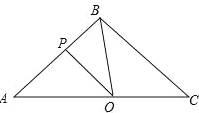
【题目】如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
(1)当x为何值时,PQ∥BC;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)△APQ能否与△CQB相似?若能,求出时间x的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A,B两点对应的有理数分别是![]() ,15,两只电子蚂蚁甲,乙分别从A,B两点同时出发相向而行,甲的速度是3个单位/秒,乙的速度是6个单位/秒
,15,两只电子蚂蚁甲,乙分别从A,B两点同时出发相向而行,甲的速度是3个单位/秒,乙的速度是6个单位/秒
(1)当乙到达A处时,求甲所在位置对应的数;
(2)当电子蚂蚁运行![]() 秒后,甲,乙所在位置对应的数分别是多少?(用含
秒后,甲,乙所在位置对应的数分别是多少?(用含![]() 的式子表示)
的式子表示)
(3)当电子蚂蚁运行![]() (
(![]() )秒后,甲,乙相距多少个单位?(用含
)秒后,甲,乙相距多少个单位?(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OM上有三点A、B、C,OC=45cm, BC=15cm, AB=30cm,已知动点P、Q同时运动,其中动点P从点O出发沿OM方向以速度2cm/s匀速运动,动点Q从点C出发沿CA方向匀速运动,当点Q运动到点A时,点Q停止运动(点P继续运动).设运动时间为t秒.

(1)求点P运动到点B所用的时间;
(2)若点Q运动速度为每秒1cm,经过多少秒时,点P和点Q的距离为30cm;
(3)当PA=2PB时,点Q恰好在线段AB的三等分点的位置,求点Q的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com