
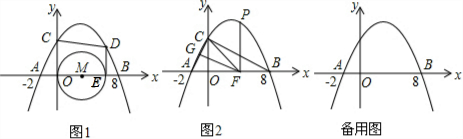
���� ��1����A��B��������������ߵĽ���ʽ�����ɵõ�����a��b�ķ����飬���a��b��ֵ���������ߵĽ���ʽ������⣻
��2������MC��MD��֤����COM�ס�MED���������������εĶ�Ӧ�ߵı���ȼ�����⣻
��3��������F������Ϊ��c��0�������BC��CF�ij�����ƽ���߷��߶γɱ������������FG�ij���Ȼ�������������ζ�Ӧ�߳ɱ��������ɵ�FC2=BC•FG����ɵõ�����c��һԪ���η��̣��ⷽ�̼�����ô𰸣�
��� �⣺��1������֪�У�$\left\{\begin{array}{l}{4a-2b+4=0}\\{64a+8b+4=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{3}{2}}\end{array}\right.$��
�������ߵĽ���ʽ�ǣ�y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
��2����D��x��y������x��0��y��0����
��E��x��0����M��$\frac{1}{2}$x��0�����ɣ�1��֪C��0��4����ͼ1 ������MC��MD��
������MC��MD��
��DE��CD���O����
���OCM=��MCD����CDM=��EDM��
���CMD=90�㣬
���COM�ס�MED��
��$\frac{CO}{ME}$=$\frac{OM}{ED}$��
��$\frac{4}{\frac{x}{2}}$=$\frac{\frac{x}{2}}{y}$��
�֡�D�����������ϣ��������ʽy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
��x=$\frac{12��4\sqrt{29}}{5}$��
�֡�x��0��
��x=$\frac{12+4\sqrt{29}}{5}$��
��E��������ǣ���$\frac{12+4\sqrt{29}}{5}$��0����
��3�����ڣ�
��BC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$��
��F��c��0����
��FG��BC��
��$\frac{FG}{BC}$=$\frac{AF}{AB}$��
��$\frac{FG}{4\sqrt{5}}$=$\frac{c+2}{10}$��
��FG=$\frac{2\sqrt{5}}{5}$��c+2����CF=$\sqrt{{c}^{2}+{4}^{2}}$��
Ҫʹ��BCF�ס�CFG��
��$\frac{CF}{BC}$=$\frac{FG}{FC}$����FC2=BC•FG��
�ɵã�16+c2=4$\sqrt{5}$��$\frac{2\sqrt{5}}{5}$��c+2����
��ã�c=0��c=8����B�غ���ȥ����
��F��0��0����
��x=0ʱ��y=-$\frac{1}{4}$��02+$\frac{3}{2}$��0+4=4��
�ʴ��ڵ�P������Ϊ��0��4����
���� ���⿼���˴���ϵ��������κ����Ľ���ʽ�Լ����������ε��ж������ʣ��Լ�ƽ���߷��߶γɱ���������֪ʶ����ȷ��õ�CD���M����ʱD��������ǹؼ���


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
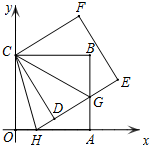 ��ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������OCBA�Ƶ�C��ʱ����ת�Ƕ�һ����Ƕ��������õ�������DCFE��ED���߶�AB���G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��
��ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������OCBA�Ƶ�C��ʱ����ת�Ƕ�һ����Ƕ��������õ�������DCFE��ED���߶�AB���G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
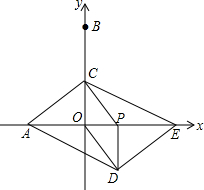 ��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ��ǣ�-2��0������0��4��������P��O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C��ÿ��2����λ���ٶ���y���ϴӵ�B�����˶�����Oֹͣ����Cֹͣ�˶�ʱ��PҲ��ֹ֮ͣ�˶�����CP��COΪ�ڱ߹���ƽ���ı���PCOD�����߶�OP���ӳ��߳�ȡ��E��ʹ��PE=2�����P���˶�ʱ��Ϊt�룮
��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ��ǣ�-2��0������0��4��������P��O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C��ÿ��2����λ���ٶ���y���ϴӵ�B�����˶�����Oֹͣ����Cֹͣ�˶�ʱ��PҲ��ֹ֮ͣ�˶�����CP��COΪ�ڱ߹���ƽ���ı���PCOD�����߶�OP���ӳ��߳�ȡ��E��ʹ��PE=2�����P���˶�ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 27�� | B�� | $\frac{27}{4}$�� | C�� | 9�� | D�� | $\frac{9}{4}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �������������/kg | ÿǧ�˼۸�/Ԫ |
| ������10kg | 6Ԫ |
| 10kg���ϵ�������20kg | 5Ԫ |
| 20kg���� | 4.6Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com