
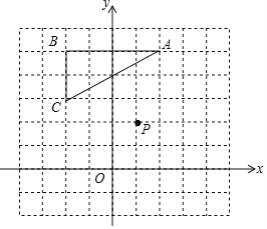
【题目】在如图所示的网格纸中,建立了平面直角坐标系xOy,点P(1,2),点A(2,5),B(-2,5),C(-2,3).
(1)以点P为对称中心,画出△A′B′C′,使△A′B′C′与△ABC关于点P对称,并写出下列点的坐标:B′________,C′________;
(2)多边形ABCA′B′C′的面积是__________.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4).则△ABC的外接圆的圆心坐标为 , △ABC的外接圆在x轴上所截的弦长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某校开展了“书香校园”、“书香家庭”的活动.学校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:


(1)这次随机调查了 名学生,统计表中d= ;
(2)假如以此统计表绘出扇形统计图,则武侠小说对应的圆心角是 °;
(3)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
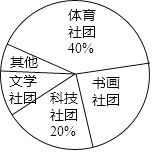
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为 ;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置. 
(1)旋转中心是点 , 旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
(1)求证:四边形PMEN是平行四边形;
(2) 当AP为何值时,四边形PMEN是菱形?并给出证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,联结AF、BE交于点G. 
(1)求证:△CAF∽△CBE;
(2)若AE:EC=2:1,求tan∠BEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组开展了一次课外活动,过程如下:
如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:AP=CQ;
(2)如图②,小明在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并证明.
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC的延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△ DEQ的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com