
| 层数 | 1 | 2 | 3 | 4 | … | n |
| 所含小三角形的个数 | 1 | 4 | 9 | 16 | … | 4n-3 |
| 所需小木棒的根数 | 3 | 9 | 18 | 30 | … | $\frac{3}{2}$n(n+1) |
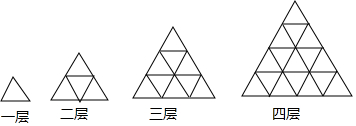
分析 分别列出一层、二层、三层、四层这四个图形中所含小三角形个数和所需小木棒的根数,得出n层时,所含小三角形个数为n2,所需小木棒的根数为3×(1+2+…+n),即可完成表格.
解答 解:∵一层时,所含小三角形个数为1,所需小木棒的根数为3,
二层时,所含小三角形个数为4=22,所需小木棒的根数为9=3×(1+2),
三层时,所含小三角形个数为9=32,所需小木棒的根数为18=3×(1+2+3),
四层时,所含小三角形个数为16=42,所需小木棒的根数为30=3×(1+2+3+4),
…
∴n层时,所含小三角形个数为n2,所需小木棒的根数为3×(1+2+…+n)=3×$\frac{n(n+1)}{2}$=$\frac{3}{2}$n(n+1),
完成表格如下:
| 层数 | 1 | 2 | 3 | 4 | … | n |
| 所含小三角形的个数 | 1 | 4 | 9 | 16 | … | 4n-3 |
| 所需小木棒的根数 | 3 | 9 | 18 | 30 | … | $\frac{3}{2}$n(n+1) |
点评 本题主要考查图形的变化规律,根据简单图形中所含小三角形个数和所需小木棒的根数,总结出一般规律是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
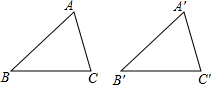 如图,已知AC=A′C′,∠C=∠C′,若△ABC≌△A′B′C′,还需要添加( )
如图,已知AC=A′C′,∠C=∠C′,若△ABC≌△A′B′C′,还需要添加( )| A. | BC=B′C′ | B. | ∠B=∠B′ | C. | ∠A=∠A′ | D. | 以上都可以 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
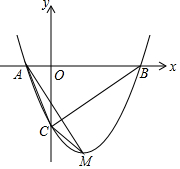 如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于点A,B,与y轴交于点C
如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于点A,B,与y轴交于点C查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com