
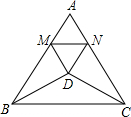
 如图,△ABC是边长为5的等边三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M、N分别在AB、AC上,连接MN,则△AMN的周长为5.
如图,△ABC是边长为5的等边三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M、N分别在AB、AC上,连接MN,则△AMN的周长为5. 分析 作辅助线,构建30°角的直角三角形,证明Rt△BDQ≌Rt△CDP得DQ=DP,再证明Rt△DQM≌Rt△DPK和△MDN≌△KDN,得MN=KN和QM=PK,利用三角形的周长公式代入可得结果.
解答 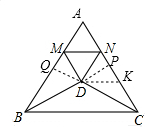 解:延长CD、BD,分别交AB于Q,交AC于P,在AC上取一点K,使KP=QM,连接DK,
解:延长CD、BD,分别交AB于Q,交AC于P,在AC上取一点K,使KP=QM,连接DK,
∵△BDC是顶角为120°的等腰三角形,
∴BD=CD,∠DBC=∠DCB=30°,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠BPC=∠CQB=90°,
∴PC=$\frac{1}{2}$BC,BQ=$\frac{1}{2}$BC,
∴PC=BQ=AQ=AP=$\frac{1}{2}$×5=$\frac{5}{2}$,
在Rt△BDQ和Rt△CDP中,
∵$\left\{\begin{array}{l}{BD=CD}\\{BQ=CP}\end{array}\right.$,
∴Rt△BDQ≌Rt△CDP(HL),
∴DQ=PD,
同理得Rt△DQM≌Rt△DPK,
∴DM=DK,∠QDM=∠PDK,
∵∠BDQ=60°,∠MDN=60°,
∴∠QDM+∠NDP=60°,
∴∠PDK+∠NDP=60°,
即∠NDK=60°,
∴∠NDK=∠MDN=60°,
∵ND=ND,
∴△MDN≌△KDN,
∴MN=NK=NP+PK,
∴△AMN的周长=AM+AN+MN=AM+AN+NP+PK=AM+AN+NP+QM=AP+AQ=$\frac{5}{2}$+$\frac{5}{2}$=5,
故答案为:5.
点评 本题主要考查了三角形全等的性质和判定、等腰三角形的性质和判定及30°的直角三角形的性质,熟练掌握三角形全等的判定是关键,尤其是直角三角形的特殊判定方法,本题应用了两次证明全等,要熟练掌握.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
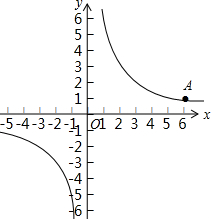 在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象过点A(6,1).
在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象过点A(6,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2017 | B. | 2016 | C. | 2017! | D. | 2016! |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不可能10次正面朝上 | B. | 必有5次正面朝上 | ||
| C. | 可能有8次正面朝上 | D. | 掷2次必有1次正面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com