
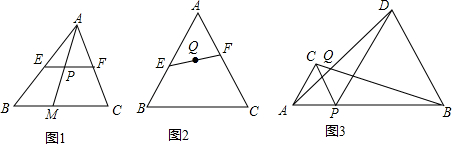
分析 阅读理解:根据轨迹的定义可知,动点P的运动轨迹是线段EF.
知识应用:如图1中,作△ABC的中位线MN,作EG∥AC交NM的延长线于G,EF与MN交于点Q′,△GQ′E≌△NQ′F,推出Q、Q′重合即可解决问题.
拓展提高:如图2中,(1)只要证明△APD≌△CPB,推出∠DQG=∠BPG=60°结论解决问题.(2)由(1)可知点P的运动轨迹是$\widehat{AB}$,设弧AB所在圆的圆心为O,Z 圆上任意取一点M,连接AM,BM,则∠M=60°,作OH⊥AB于H,则AH=BH=3,OH=$\sqrt{3}$,OB=2$\sqrt{3}$,利用弧长公式即可解决.
解答 阅读理解:根据轨迹的定义可知,动点P的运动轨迹是线段EF.
故答案为线段EF.
知识应用:如图1中,作△ABC的中位线MN,作EG∥AC交NM的延长线于G,EF与MN交于点Q′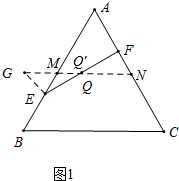
∵△ABC是等边三角形,MN是中位线,
∴AM=BM=AN=CN,
∵AF=BE,
∴EM=FN,
∵MN∥BC,
∴∠AMN=∠B=∠GME=60°,
∵∠A=∠GEM=60°,
∴△GEM是等边三角形,
∴EM=EG=FN,
在△GQ′E和△NQ′F中,
$\left\{\begin{array}{l}{∠GQ′E=∠NQ′F}\\{∠G=∠FNQ′}\\{GE=FN}\end{array}\right.$,
∴△GQ′E≌△NQ′F,
∴EQ′=FQ′,
∵EQ=QF,
′点Q、Q′重合,
∴点Q在线段MN上,
∴段EF中点Q的运动轨迹是线段MN,
MN=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4.
∴线段EF中点Q的运动轨迹的长为4.
拓展提高:如图2中,
(1)∵△APC,△PBD都是等边三角形,
∴AP=PC,PD=PB,∠APC=∠DPB=60°,
∴∠APD=∠CPB,
在△APD和△CPB中,
$\left\{\begin{array}{l}{AP=PC}\\{∠APD=∠CPB}\\{DP=BP}\end{array}\right.$,
∴△APD≌△CPB,
∴∠ADP=∠CBP,设BC与PD交于点G,
∵∠QGD=∠PGB,
∴∠DQG=∠BPG=60°,
∴∠AQB=180°-∠DQG=120°
(2)由(1)可知∠AQB=120°是定值,
所以点Q的运动轨迹是$\widehat{AB}$,设弧AB所在圆的圆心为O,在圆上任意取一点M,连接AM,BM,
则∠M=60°,
∴∠AOB=2∠M=120°,作OH⊥AB于H,则AH=BH=3,OH=$\sqrt{3}$,OB=2$\sqrt{3}$,
∴弧AB的长=$\frac{120°×π×2\sqrt{3}}{180°}$=$\frac{4\sqrt{3}}{3}$π.
∴动点Q运动轨迹的长$\frac{4\sqrt{3}}{3}$π.
点评 本题考查三角形综合题、全等三角形的判定和性质、圆的有关性质、弧长公式等知识,解题的关键是理解轨迹的意义,学会添加常用辅助线,学会探究找到轨迹的方法,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x度时,应交电费为y元.具体收费情况如折线图所示,请根据图象回答下列问题:
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x度时,应交电费为y元.具体收费情况如折线图所示,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成证明,说明理由.已知:如图,BC∥DE,点E在AB边上,DE、AC交于点F,∠1=∠2,∠3=∠4,求证AE∥CD.
完成证明,说明理由.已知:如图,BC∥DE,点E在AB边上,DE、AC交于点F,∠1=∠2,∠3=∠4,求证AE∥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com