
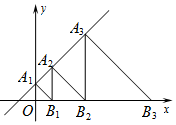
 如图,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2017等于( )
如图,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2017等于( )| A. | 24030 | B. | 24031 | C. | 24032 | D. | 24033 |
分析 根据已知条件得到△△OA1B1,△B1A2B2,△B2A3B3是等腰直角三角形,根据最新的解析式得到A1(0,1),求得B1(1,0),得到OB1=OA1=1,根据三角形的面积公式得到S1=$\frac{1}{2}$×1×1=$\frac{1}{2}$×12,同理S2=$\frac{1}{2}$×2×2=$\frac{1}{2}×$22,S3=$\frac{1}{2}×$4×4=$\frac{1}{2}×$42;…得到Sn=$\frac{1}{2}×$22n-2=22n-3,于是得到结论.
解答 解:∵OB1=OA1;过点B1作A2B1⊥x轴,B1B2=B1A2;A3B2⊥x轴,B2B3=B2A3;…
∴△△OA1B1,△B1A2B2,△B2A3B3是等腰直角三角形,
∵y=x+1交y轴于点A1,
∴A1(0,1),
∴B1(1,0),
∴OB1=OA1=1,
∴S1=$\frac{1}{2}$×1×1=$\frac{1}{2}$×12,
同理S2=$\frac{1}{2}$×2×2=$\frac{1}{2}×$22,S3=$\frac{1}{2}×$4×4=$\frac{1}{2}×$42;…
∴Sn=$\frac{1}{2}×$22n-2=22n-3,
∴S2017=22×2017-3=24031,
故选B.
点评 本题考查了一次函数图象上点的坐标特征,等腰直角三角形的性质,三角形面积的计算,正确的识别图形是解题的关键.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$ | B. | 4$\sqrt{3}$-$\sqrt{2}$ | C. | 5$\sqrt{2}$-4$\sqrt{3}$ | D. | 5$\sqrt{2}$+4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | △ABC中,∠A、∠B、∠C的对边分别为a、b、c.若a2+b2=c2 则∠B=90° | |
| B. | 如果一个三角形两边的平方差等于第三边的平方,那么这个三角形是直角三角形 | |
| C. | 直角三角形中,两条边的平方和等于第三边的平方 | |
| D. | △ABC中,若a=3、b=4则c=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
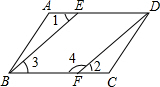 如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:
如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
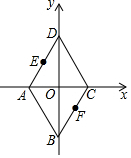 以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,若AD的中点E的坐标为(a,b),则BC的中点F的坐标为(-a,-b).
以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,若AD的中点E的坐标为(a,b),则BC的中点F的坐标为(-a,-b).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com