
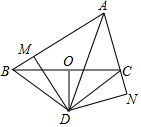
 如图,△ABC中,点O在边BC上,OD垂直平分BC,AD平分∠BAC,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
如图,△ABC中,点O在边BC上,OD垂直平分BC,AD平分∠BAC,过点D分别作DM⊥AB于点M,DN⊥AC于点N.分析 连DB、DC,根据角平分线性质得DM=DN;根据垂直平分线的性质得DB=DC;再根据“HL”定理证明Rt△EFB≌Rt△EGC,从而得BM=CN.
解答 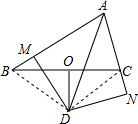 证明:连接BD,CD,如图,
证明:连接BD,CD,如图,
∵O是BC的中点,DO⊥BC,
∴OD是BC的垂直平分线,
∴BD=CD,
∵AD是∠BAC的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△BMD和Rt△CND中,$\left\{\begin{array}{l}{BD=CD}\\{DM=DN}\end{array}\right.$,
∴Rt△BMD≌Rt△CND(HL),
∴BM=CN.
点评 本题考查了角平分线性质和垂直平分线的性质,利用了三角形全等的判定和性质解题.正确作出辅助线是解答本题的关键,属于中考常考题型.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
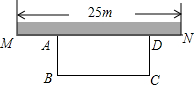 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知y与x-3成正比例,当x=4时,y=3.
已知y与x-3成正比例,当x=4时,y=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
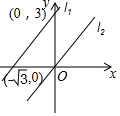 如图,直线L1过点(0,3),(-$\sqrt{3}$,0).
如图,直线L1过点(0,3),(-$\sqrt{3}$,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com