
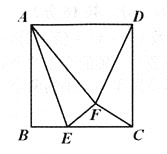
【题目】如图,点E是边长为2的正方形ABCD的边BC上的一动点(不与端点重合),将△ABE沿AE翻折至△AFE的位置,若△CDF是等腰三角形,则BE=________.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板![]() 与
与![]() (其中
(其中![]() ,
,![]() ,
,![]() )如图摆放,
)如图摆放,![]() 中
中![]() 所对的直角边与
所对的直角边与![]() 的斜边恰好重合。以
的斜边恰好重合。以![]() 为直径的圆经过点C,且与
为直径的圆经过点C,且与![]() 相交于点E,连接
相交于点E,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于F.
于F.
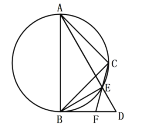
(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 与
与![]() 的面积的比值.
的面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 问题与探索
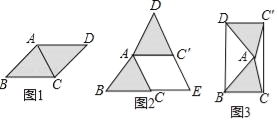
问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 .
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东55方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
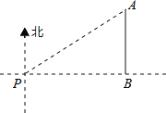
A.2cos55o海里B.![]() 海里C.2sin55海里D.
海里C.2sin55海里D.![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学利用寒假30天时间贩卖草莓,了解到某品种草莓成本为10元/千克,在第![]() 天的销售量与销售单价如下(每天内单价和销售量保持一致):
天的销售量与销售单价如下(每天内单价和销售量保持一致):
销售量 |
|
销售单价 | 当 |
当 |
设第![]() 天的利润
天的利润![]() 元.
元.
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?注:利润=(售价-成本)×销售量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设D为锐角△ABC内一点,∠ADB=∠ACB+90°,过点B作BE⊥BD,BE=BD,连接EC.
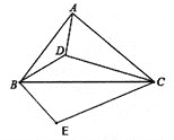
(1)求∠CAD+∠CBD的度数;
(2)若![]() ,
,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城市化建设的发展,交通拥堵成为上班高峰时难以避免的现象.为了解龙泉驿某条道路交通拥堵情况,龙泉某中学同学经实地统计分析研究表明:当![]() 时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
(1)当![]() 时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
(2)为使该道路上车流速度大于40千米/小时且小于60千米/小时,应控制该道路上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过该道路上某观测点的车辆数,即:车流量=车流速度×车流密度.当![]() 时,求该道路上车流量y的最大值.此时车流速度为多少?
时,求该道路上车流量y的最大值.此时车流速度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
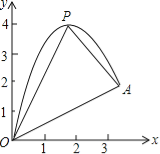
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com