在数学课上，老师给出以下条件和问题，要求同学们探索并得出结论：
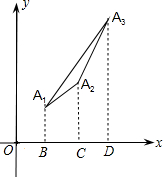
（1）点A1，A2，A3是抛物线y=2x2图象上的三点，若A1，A2，A3三点的横坐标从左至右依次为1，2，3，求△A1A2A3的面积；
（2）若将（1）中的抛物线改为y=2x2-4x+7，其他条件不变，那么△A1A2A3的面积变不变？请求出△A1A2A3的面积；
（3）若将抛物线改为y=ax2+bx+c （a＞0），其他条件不变，那么△A1A2A3的面积又是多少呢？请说明理由；
（4）从中你发现了什么规律？请用一句话简单归纳．
解：（1）当点A
1 A
2 A
3是抛物线y=2x
2图象上的三点，
若A
1，A
2，A
3，三点的横坐标从左至右依次为1，2，3，
∴A
1，A
2，A
3三点的纵坐标从左至右依次为2，8，18，
∴S
△A1A2A3=S
梯形A1BDA3-S
梯形A1BCA2-S
梯形A2CDA3=
×（2+18）×2-
×（8+18）×1-
×（2+8）×1=2；
（2）若将（1）中的抛物线改为y=2x
2-4x+7，
其他条件不变，那么△A
1A
2A
3的面积不变，即：△A
1A
2A
3的面积为2；
（3）若将抛物线改为y=ax
2+bx+c （a＞0），
∵若A
1，A
2，A
3，三点的横坐标从左至右依次为1，2，3，
∴A
1，A
2，A
3三点的纵坐标从左至右依次为a+b+c，4a+2b+c，9a+3b+c，
∴S
△A1A2A3=S
梯形A1BDA3-S
梯形A1BCA2-S
梯形A2CDA3=
×（a+b+c+9a+3b+c）×2-
×（a+b+c+4a+2b+c）×1-
×（4a+2b+c+9a+3b+c）×1=a；
∴△A
1A
2A
3的面积为a；
（4）从中发现规律：若点A
1 A
2 A
3是抛物线y=ax
2+bx+c图象上的三点，
且A
1，A
2，A
3，三点的横坐标从左至右依次为1，2，3，
则△A
1A
2A
3的面积等于二次项系数的绝对值．----
分析：（1）由点A
1，A
2，A
3是抛物线y=2x
2图象上的三点，若A
1，A
2，A
3三点的横坐标从左至右依次为1，2，3，即可求得A
1，A
2，A
3三点的纵坐标，又由S
△A1A2A3=S
梯形A1BDA3-S
梯形A1BCA2-S
梯形A2CDA3，即可求得△A
1A
2A
3的面积；
（2）解法同（1），即可得其他条件不变，那么△A
1A
2A
3的面积不变，即△A
1A
2A
3的面积为2；
（3）由点A
1，A
2，A
3是抛物线y=ax
2+bx+c （a＞0）图象上的三点，若A
1，A
2，A
3三点的横坐标从左至右依次为1，2，3，即可求得A
1，A
2，A
3三点的纵坐标，又由S
△A1A2A3=S
梯形A1BDA3-S
梯形A1BCA2-S
梯形A2CDA3，即可求得△A
1A
2A
3的面积；
（4）可得规律：若点A
1 A
2 A
3是抛物线y=ax
2+bx+c图象上的三点，且A
1，A
2，A
3，三点的横坐标从左至右依次为1，2，3，则△A
1A
2A
3的面积等于二次项系数的绝对值
点评：此题考查了点与二次函数的关系以及三角形面积的求解方法．此题难度较大，解题的关键是抓住△A
1A
2A
3的面积的求解方法，注意S
△A1A2A3=S
梯形A1BDA3-S
梯形A1BCA2-S
梯形A2CDA3，注意数形结合思想的应用．
