
【题目】如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据已知条件易证∠BFO=∠DEO,∠FBO=∠EDO,OB=OD,再利用AAS证明△BOF≌△DOE即可;(2)连接BE,设AE=xcm,由EB=ED=AD﹣AE=(4﹣x)cm,在Rt△ABE中,根据AB2+AE=BE2,构建方程即可解决问题.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFO=∠DEO,∠FBO=∠EDO,
又∵O是BD中点,
∴OB=OD,
∴△BOF≌△DOE(ASA).
(2)连接BE.
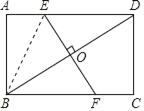
∵EF⊥BD,O为BD中点,
∴EB=ED,
设AE=xcm,由EB=ED=AD﹣AE=(4﹣x)cm,
在Rt△ABE中,AB=3cm,
根据勾股定理得:AB2+AE=BE2,即9+x2=(4﹣x)2,
解得:x=![]() ,
,
∴AE的长是 ![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
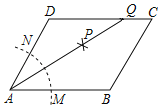
【题目】如图,在平行四边形ABCD中,按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;
②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;
MN的长为半径作弧,两弧相交于点P;
③作AP射线,交边CD于点Q.
若QC=1,BC=3,则平行四边形ABCD周长为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
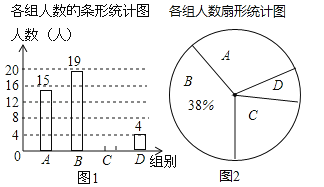
【题目】小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
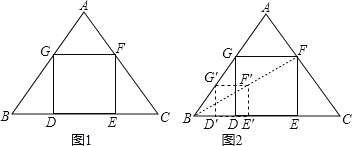
【题目】如图,△ABC是一块等边三角形的废铁片,其中AB=AC=10![]() ,BC=12
,BC=12![]() .利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F. G分别落在AC、AB上.
.利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F. G分别落在AC、AB上.
(1)小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.请你帮小聪求出正方形的边长.
(2)小明想:不求正方形的边长也能画出正方形.具体作法是:
①在AB边上任取一点G′,如图2作正方形G′D′E′F′;
②连接BF′并延长交AC于点F;
③过点F作FE∥F′E′交BC于点E,FG∥F′G′交AB于点G,GD∥G′D′交BC于点D,则四边形DEFG即为所求的正方形.你认为小明的作法正确吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦AC为6cm,
(1)用尺规作图画出∠ACB的平分线交⊙O于点D.(不要写作法,保留作图痕迹)
(2)分别连接点AD和BD,求弦BC、AD、BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关公,作为运城乃至山西的一张名片,吸引了来自世界各地的游客,在运城西南![]() 公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高
公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高![]() 米,象征关公享年
米,象征关公享年![]() 岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图,
岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图,![]() 代表底座的高,坡顶
代表底座的高,坡顶![]() 与底座底部
与底座底部![]() 处在同一水平面上,该游客在斜坡底
处在同一水平面上,该游客在斜坡底![]() 处测得该底座顶端
处测得该底座顶端![]() 的仰角为
的仰角为![]() ,然后他沿着坡度为
,然后他沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该底座顶端
处又测得该底座顶端![]() 的仰角为
的仰角为![]() .求:
.求:
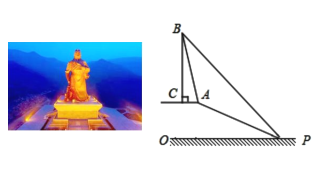
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 求底座
求底座![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的引桥部分的示意图,梯面AD、BE相互平行,且与地面成37°的夹角,DE是一段水平歇台,离地面高度3米.已知天桥高度BC为4.8米,引桥水平跨度AC为8米,求梯面AD、BE及歇台DE的长.(参考数据:![]() ,结果保留两位小数)
,结果保留两位小数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com