
【题目】解下列不等式(组)
(1)![]()
(2)![]()
(3)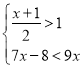 (并在数轴上表示出解集 )
(并在数轴上表示出解集 )
(4)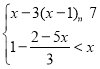 (解不等式组并写出整数解)
(解不等式组并写出整数解)
【答案】(1) x≥4;(2) x≥2; (3) x>1,数轴见解析;(4)-2≤ x< -![]() ;整数解为 -2,-1
;整数解为 -2,-1
【解析】
(1)先去括号,再移项,合并同类项,系数化为1即可.
(2)先去分母,再去括号,移项,合并同类项,系数化为1即可.
(3)先解两个不等式,再求公共部分即可;
(4)先解两个不等式,再求公共部分即可;.
(1)![]()
104x+12≤2x2;
2x+4x≥10+12+2,
6x≥24,
x≥4;
(2)![]()
![]()
12x+12+2x-4≤21x-6
-7x≤-14
x≥2
(3)解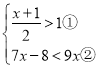
解①得x>1,
解②得x>-4,
在数轴上表示为
![]()
∴不等式组的解集为x>1;
(4)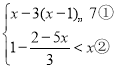
解①得x≥-2,
解②得x<-![]() ,
,
∴不等式组的解集为-2≤ x< -![]()
故整数解为-2,-1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
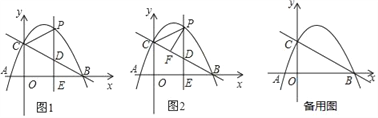
【题目】如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)、B(4,0)两点,与y轴交于点C,且OC=3OA.点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.
(1)求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,求过点P作PF⊥BC于点F,试问△PDF的周长是否有最大值?如果有,请求出其最大值,如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四边形CDPQ是否成为菱形?如果能,请求出此时点P的坐标,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
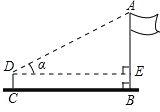
【题目】某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示:
数据组别 | CD的长(m) | BC的长(m) | 仰角α | AB的长(m) |
第一组 | 1.59 | 13.2 | 32° | 9.8 |
第二组 | 1.58 | 13.4 | 31° | 9.6 |
第三组 | 1.57 | 14.1 | 30° | 9.7 |
第四组 | 1.56 | 15.2 | 28° |
(1)利用第四组学生测量的数据,求旗杆AB的高度(精确到0.1m);
(2)四组学生测量旗杆高度的平均值约为 m(精确到0.1m).
(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字![]() ,2,3且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为
,2,3且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为![]() 的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为
的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为![]() 的值,两次结果记为
的值,两次结果记为![]() .
.
(1)请你帮他们用画树状图或列表的方法表示![]() 所有可能出现的结果;
所有可能出现的结果;
(2)若将记录结果![]() 看成平面直角坐标系中的一点,求
看成平面直角坐标系中的一点,求![]() 是第一象限内的点的概率.
是第一象限内的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.
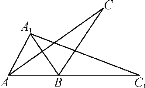
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一节数学课后,老师布置了一道课后练习题:
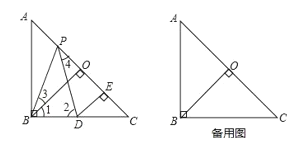
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
理清思路,本题证明的思路可用下列框图表示:
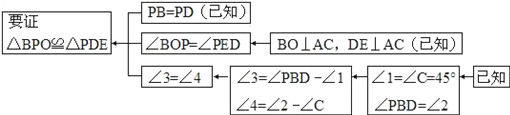
根据上述思路,请你完成下列问题.
(1)若BP平分∠ABO,其余条件不变.求证:AP=CD.
(2)若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系,并证明得出的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点M在BC边上,且BM=![]() BC,AM与BD相交于点N,那么S△BMN:S平行四边形ABCD为( )
BC,AM与BD相交于点N,那么S△BMN:S平行四边形ABCD为( )

A.1:3B.1:9C.1:12D.1:24
查看答案和解析>>
科目:初中数学 来源: 题型:
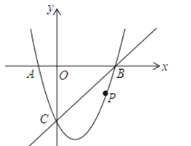
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点,过点P作平行于y轴的直线PM,交线段BC于M,当△PCM是以PM为腰的等腰三角形时,点P的坐标是( )
A.(2,-3)或(![]() +1,—2)B.(2,-3)或(
+1,—2)B.(2,-3)或(![]() ,-1-2
,-1-2![]() )
)
C.(2,-3)或(![]() ,-1-2
,-1-2![]() )D.(2,-3)或(3-
)D.(2,-3)或(3-![]() ,2-4
,2-4![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com