
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
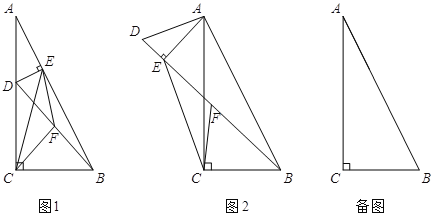
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
【答案】(1)k=1(2)证明![]() ,则可得
,则可得![]() . (3)当点D在靠近点C的
. (3)当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为![]()
【解析】试题分析:解:(1)k=1; .
(2)如图2,过点C作CE的垂线交BD于点G,设BD与AC的交点为Q.
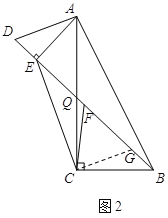
由题意,tan∠BAC=![]() ,
,
∴![]() .
.
∵D、E、B三点共线,
∴AE⊥DB.
∵∠BQC=∠AQD,∠ACB=90°,
∴∠QBC=∠EAQ.
∵∠ECA+∠ACG=90°,∠BCG+∠ACG=90°,
∴∠ECA=∠BCG.
∴![]() .
.
∴![]() .
.
∴GB=DE.
∵F是BD中点,
∴F是EG中点.
在![]() 中,
中, ![]() ,
,
∴![]() . . .
. . .
(3)情况1:如图,当AD= ![]() 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,
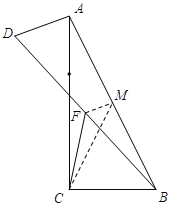
∵∠ACB=90°, tan∠BAC=![]() ,且BC= 6,
,且BC= 6,
∴AC=12,AB=![]() .
.
∵M为AB中点,∴CM=![]() ,
,
∵AD= ![]() ,
,
∴AD=![]() .
.
∵M为AB中点,F为BD中点,
∴FM= ![]() = 2.
= 2.
∴当且仅当M、F、C三点共线且M在线段CF上时CF最大,此时CF=CM+FM=![]() .
.
情况2:如图,当AD= ![]() 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,
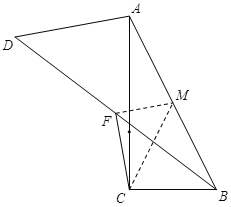
类似于情况1,可知CF的最大值为![]() .
.
. 6分
综合情况1与情况2,可知当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现了解情况如下:甲、乙两家商店出售两种同样品牌的笔记本和钢笔.笔记本定价为每本20元,钢笔每支定价5元,经洽谈后,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.七年级需笔记本20本,钢笔若干支(不小于20支).问:
(1)如果购买钢笔![]() (
(![]() 不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
(2)当购买钢笔多少支时,在两店购买付款一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
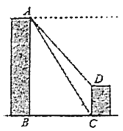
【题目】如图,甲、乙两座建筑物的水平距离![]() 为
为![]() ,从甲的顶部
,从甲的顶部![]() 处测得乙的顶部
处测得乙的顶部![]() 处的俯角为48°,测得底部
处的俯角为48°,测得底部![]() 处的俯角为58°,求乙建筑物
处的俯角为58°,求乙建筑物![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .结果取整数)
.结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
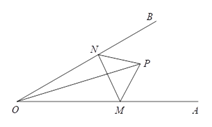
【题目】如图,点![]() 是
是![]() 内任意一点,
内任意一点,![]() ,点
,点![]() 和点
和点![]() 分别是射线
分别是射线![]() 和射线
和射线![]() 上的动点
上的动点![]() 周长的最小值是
周长的最小值是![]() ,则
,则![]() 的度数是( )
的度数是( )
A. 25度 B. 30度 C. 35度 D. 40度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,![]() 的平分线AE交CD于点F交BC的延长线于点E.
的平分线AE交CD于点F交BC的延长线于点E.
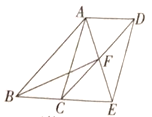
(1)求证:![]() ;
;
(2)连接BF、AC、DE,当![]() 时,求证:四边形ACED是平行四边形.
时,求证:四边形ACED是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始的4分内只进水不出水,在随后的若干分内既进水又出水,之后只有出水不进水,每分钟的进水量和出水量是两个常数,容器内的水量![]() (单位:升)与时间
(单位:升)与时间![]() (单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,
(单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,![]() 的值为______.
的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平画直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 沿
沿![]() 轴向右平移2个单位长度交
轴向右平移2个单位长度交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() .
.

(1)直接写出直线![]() 的解析式为______,
的解析式为______,![]() ______.
______.
(2)在直线![]() 上存在点
上存在点![]() ,使
,使![]() 是
是![]() 的中线,求点
的中线,求点![]() 的坐标;
的坐标;
(3)如图2,在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,若关于 x 的一元一次方程 ax=b 的解为 x=ba,则称该方程的为差解方程,例如:3x=![]() 的解为x=
的解为x=![]() 且
且![]() =
=![]() -3,则该方程3x=
-3,则该方程3x=![]() 就是差解方程.
就是差解方程.
请根据以上规定解答下列问题
(1)若关于 x 的一元一次方程-5x=m+1 是差解方程,则 m=_____.
(2)若关于 x 的一元一次方程 2x=ab+3a+1 是差解方程,且它的解为 x=a,求代数式(ab+2)2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
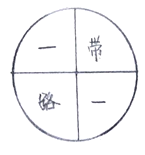
【题目】“一带一路”是指“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.数学兴趣小组设计了一个可以自由转动的均匀转盘,转盘被分成相等的4份,且每份分别标有“一”、“带”、“一”、“路”的字.任意转动转盘,转盘停止后,指针都会指向其中的一个字(如果指针恰好停在等分线上,那么重新转一次,直到指针指向转盘中四等份中的某一份为止)
(1)转动转盘一次,求指针恰好指到“一”字的概率;
(2)连续转动转盘两次,请用列表或者画树状图的方法求指针两次都指向“一”字的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com