
| A. | 梯形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
分析 根据三角形的中位线定理和菱形的判定,可得顺次连接对角线相等的四边形各边中点所得四边形是菱形解答即可.
解答  解:已知,如图:
解:已知,如图:
E、F、G、H分别是四边形ABCD各边AB、BC、CD、DA的中点,对角线AC=BD,
求证:四边形EFGH是菱形.
证明:∵E、F、G、H分别是四边形ABCD各边AB、BC、CD、DA的中点,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
又∵EF=$\frac{1}{2}$AC,EH=$\frac{1}{2}$AC,AC=BD,
∴EH=EF,
∴平行四边形EFGH是菱形,
∴四边形EFGH是菱形.
故选:C.
点评 此题主要考查了中点四边形,注意:菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:
①定义;②四边相等;③对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是$\frac{5}{13}$.
如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是$\frac{5}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
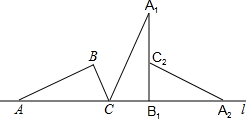 如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB=$\sqrt{3}$,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB=$\sqrt{3}$,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )| A. | ($\frac{4}{3}$+$\frac{\sqrt{3}}{2}$)π | B. | ($\frac{25}{12}$+$\frac{\sqrt{3}}{2}$)π | C. | 2π | D. | $\sqrt{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com