

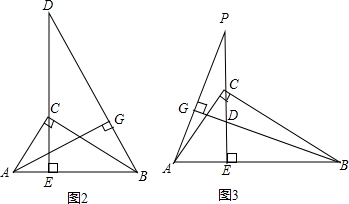
| CE |
| AE |
| BE |
| CE |
| AE |
| ED |
| EP |
| BE |
| ED•EP |
| AE |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏南京三中(六中校区)八年级下期期末数学试卷(带解析) 题型:解答题
如图1,已知,CE是Rt△ABC的斜边AB上的高,点P是CE的延长线上任意一点,BG⊥AP,
求证:(1)△AEP∽△DEB
(2) CE2=ED·EP
若点P在线段CE上或EC的延长线上时(如图2和图3),上述结论CE2=ED·EP还成立吗?若成立,请给出证明;若不成立,请说明理由.(图2和图3挑选一张给予说明即可)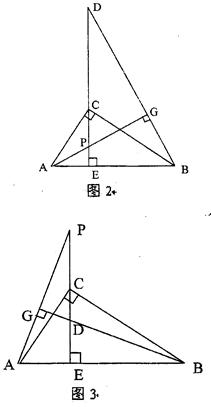
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com