
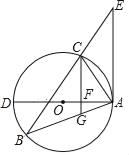
【题目】如图,⊙O是△ABC的外接圆, AD是⊙O的直径,BC的延长线于过点A的直线相交于点E,且∠B=∠EAC.
(1)求证:AE是⊙O的切线;
(2)过点C作CG⊥AD,垂足为F,与AB交于点G,若AGAB=36,tanB=![]() ,求DF的值
,求DF的值
【答案】(1)见解析;(2)4![]()
【解析】分析:(1)欲证明AE是⊙O切线,只要证明OA⊥AE即可;
(2)由△ACD∽△CFD,可得![]() ,想办法求出CD、AD即可解决问题.
,想办法求出CD、AD即可解决问题.
详解:(1)证明:连接CD.
∵∠B=∠D,AD是直径,
∴∠ACD=90°,∠D+∠1=90°,∠B+∠1=90°,
∵∠B=∠EAC,
∴∠EAC+∠1=90°,
∴OA⊥AE,
∴AE是⊙O的切线.
(2)∵CG⊥AD.OA⊥AE,
∴CG∥AE,
∴∠2=∠3,
∵∠2=∠B,
∴∠3=∠B,
∵∠CAG=∠CAB,
∴△ABC∽△ACG,
∴![]() ,
,
∴AC2=AGAB=36,
∴AC=6,
∵tanD=tanB=![]() ,
,
在Rt△ACD中,tanD=![]() =
=![]()
CD=![]() =6
=6![]() ,AD=
,AD=![]() =6
=6![]() ,
,
∵∠D=∠D,∠ACD=∠CFD=90°,
∴△ACD∽△CFD,
∴![]() ,
,
∴DF=4![]() ,
,


科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
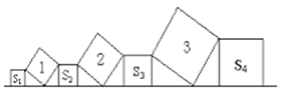
A. 5 B. 4 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
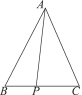
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
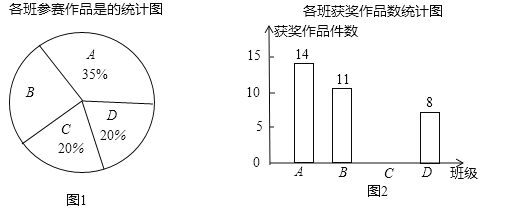
【题目】【本小题满分9分】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
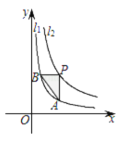
【题目】如图,函数![]() (x>0)和
(x>0)和![]() (x>0)的图象分别是
(x>0)的图象分别是![]() 和
和![]() .设点P在
.设点P在![]() 上,PA∥y轴交
上,PA∥y轴交![]() 于点A,PB∥x轴,交
于点A,PB∥x轴,交![]() 于点B,△PAB的面积为( )
于点B,△PAB的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
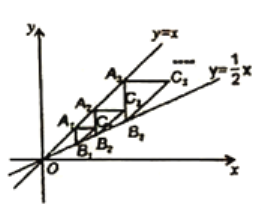
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以点
,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,再过点
,再过点![]() 作
作![]() 轴,分别交直线
轴,分别交直线![]() 和
和![]() 于
于![]() ,
,![]() 两点,以点
两点,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() 按此规律进行下去,则等腰直角
按此规律进行下去,则等腰直角![]() 的面积为_______,等腰直角
的面积为_______,等腰直角![]() 的面积为______.
的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一元二次方程中,两实根之和为1的是 ( )
A. x2—x+1=0 B. x2+x—3=0 C. 2 x2-x-1=0 D. x2-x-5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古语说:“春眠不觉晓”,每到初春时分,想必有不少人变得嗜睡,而且睡醒后精神不佳.我们可以在饮食方面进行防治,比如以下食物可防治春困:香椿、大蒜、韭菜、山药、麦片.春天即将来临时,某商人抓住商机,购进甲、乙、丙三种麦片,已知销售每袋甲种麦片的利润率为10%,每袋乙种麦片的利润率为20%,每袋丙种麦片的利润率为30%,当售出的甲、乙、丙三种麦片的袋数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙三种变片的袋数之比为3:2:1时,商人得到的总利润率为20%:那么当售出的甲、乙、丙三种麦片的袋数之比为2:3;4时,这个商人得到的总利润率为_____(用百分号表最终结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com