
 ,那么AP的长为______.
,那么AP的长为______. 是一个完全平方式,则m=______.
是一个完全平方式,则m=______.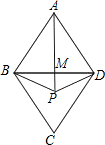
 ,BM=AB•sin30°=3,
,BM=AB•sin30°=3, ,
, ;
; ;
; 矛盾,舍去.
矛盾,舍去.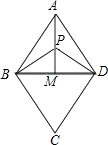
 或2
或2 .
. 或2
或2 .
. 是一个完全平方式,
是一个完全平方式, =(x+
=(x+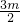 )2-
)2- m2-m+
m2-m+ ,
, m2-m+
m2-m+ =0,
=0,

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
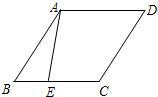
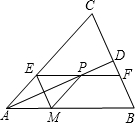 EF∥AB,分别交AC,BC于E,F点,作PM∥AC,交AB于M点,连接ME.
EF∥AB,分别交AC,BC于E,F点,作PM∥AC,交AB于M点,连接ME.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
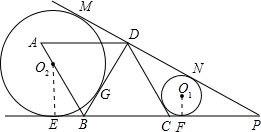 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com