
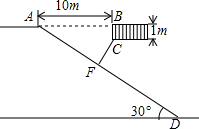
 某住宅小区为缓解停车难问题,新建了地下停车场,建筑设计师提供了地下停车场的设计示意图.按规定,停车场坡道口要张贴限高标志,以便告知车辆能否安全驶入.请根据如图,求出汽车通过坡道口的限高CF的长($\sqrt{3}$≈1.73,结果精确到0.1m).
某住宅小区为缓解停车难问题,新建了地下停车场,建筑设计师提供了地下停车场的设计示意图.按规定,停车场坡道口要张贴限高标志,以便告知车辆能否安全驶入.请根据如图,求出汽车通过坡道口的限高CF的长($\sqrt{3}$≈1.73,结果精确到0.1m). 分析 根据锐角三角函数的定义,可在Rt△ABH中解得BH的值,进而求得CH的大小;在Rt△CFH中,利用余弦的定义,即可求得CF的值.
解答 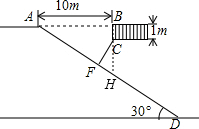 解:如图,延长BC交AD于点H,在Rt△ABH中,∠A=30°,AB=10,
解:如图,延长BC交AD于点H,在Rt△ABH中,∠A=30°,AB=10,
∴BH=ACtan30°=$\frac{10\sqrt{3}}{3}$m,
∴CH=BH-BC=($\frac{10\sqrt{3}}{3}$-1)米,
∴在Rt△CFH中,∠HCF=∠A=30°,CH=($\frac{10\sqrt{3}}{3}$-1)米,
∴DF=CHcos30°=($\frac{10\sqrt{3}}{3}$-1)×$\frac{\sqrt{3}}{2}$≈4.1m,
答:坡道口的限高DF的长是4.1m.
点评 本题考查了解直角三角形的应用,坡面坡角问题和勾股定理,解题的关键是坡度等于坡角的正切值.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 357×104 | B. | 3.57×107 | C. | 35.7×105 | D. | 3.57×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明在作线段AB的垂直平分线时,是这样操作的:分别以点A、B为圆心,大于线段AB长度一半的长为半径画弧,相交于C、D,则直线CD即为所求,连接AC、BC、BD,根据他的作图方法可知,四边形ADBC一定是( )
如图,小明在作线段AB的垂直平分线时,是这样操作的:分别以点A、B为圆心,大于线段AB长度一半的长为半径画弧,相交于C、D,则直线CD即为所求,连接AC、BC、BD,根据他的作图方法可知,四边形ADBC一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 梯形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格纸中的最小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C坐标为(0,-1)
如图,方格纸中的最小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C坐标为(0,-1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com