
【题目】已知二次函数y=x -2mx(m为常数),当-1≤x≤2时,函数y的最小值为-2,则m的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D. -
D. -![]() 或
或![]()
【答案】D
【解析】先将二次函数配方得: ![]() ,根据二次函数图象和性质可知:
,根据二次函数图象和性质可知:
对称轴![]() ,由于对称轴位置不确定,所以分m<-1, m>2, -1≤m≤2三种情况,根据二次函数y的最小值为-2,结合二次函数图象和性质进行解答, ①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-
,由于对称轴位置不确定,所以分m<-1, m>2, -1≤m≤2三种情况,根据二次函数y的最小值为-2,结合二次函数图象和性质进行解答, ①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-![]() ,②若m>2,当x=2时,y最小值=4-4m=-2,解得m=
,②若m>2,当x=2时,y最小值=4-4m=-2,解得m=![]() <2(舍),
<2(舍),
③若-1≤m≤2,当x=m时,y最小值=-![]() =-2,解得m=
=-2,解得m=![]() 或m=-
或m=-![]() <-1(舍),综上所述,m的值为-
<-1(舍),综上所述,m的值为-![]() 或
或![]() ,因此正确选项是D.
,因此正确选项是D.
y=x -2mx=(x-m) -m2.分以下3种情况:①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-![]() ;②若m>2,当x=2时,y最小值=4-4m=-2,解得m=
;②若m>2,当x=2时,y最小值=4-4m=-2,解得m=![]() <2(舍);③若-1≤m≤2,当x=m时,y最小值=-m2=-2,解得m=
<2(舍);③若-1≤m≤2,当x=m时,y最小值=-m2=-2,解得m=![]() 或m=-
或m=-![]() <-1(舍).综上所述,m的值为-
<-1(舍).综上所述,m的值为-![]() 或
或![]() ,故选D
,故选D


科目:初中数学 来源: 题型:
【题目】如图,已知线段AB、a、b.
(1)请用尺规按下列要求作图:(不要求写作法,但要保留作图痕迹)
①延长线段AB到C,使BC=a;
②反向延长线段AB到D,使AD=b.
(2)在(1)的条件下,如果AB=8cm,a=6m,b=10cm,且点E为CD的中点,求线段AE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
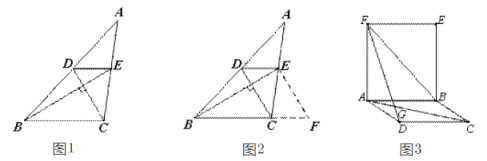
【题目】阅读下面的材料:小锤遇到一个问题:如图①,在△ABC中,DE//BC分别交AB于点D,交AC于点E,已知CD![]() BE,CD=2,BE=3,求BC+DE的值.
BE,CD=2,BE=3,求BC+DE的值.
小锤发现,过点E作EF![]() DC,交BC的延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决.
DC,交BC的延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决.
(1)请按照上述思路完成小锤遇到的问题;
(2)参考小锤思考问题的方法,解决下面的问题:如图②,四边形ABCD是平行四边形,四边形ABEF是矩形,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() |,
|,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:(1)因为![]() ,所以
,所以![]() ______;
______;
因为![]() ,所以
,所以![]() ______;
______;
又因为![]() ,
,
所以当![]() ______时,
______时,![]() ______;
______;
或当![]() ______时,
______时,![]() ______,
______,
∴![]() ______或_______.
______或_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,
,![]() .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
.将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
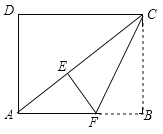
(1)求线段AC的长.
(2)求线段EF的长.
(3)点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出![]() ,并直接写出线段DH的长.
,并直接写出线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表所示是2019年元月的月历表.下列结论:
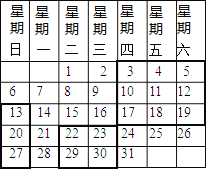
①每一竖列上相邻的两个数,下面的数比上面的数大7;
②可以框出一竖列上相邻的三个数(如图所示),这三个数的和是24;
③不可以框出一个2×2的矩形块的四个数(如图所示),这四个数的和是82;
④任意框出一个3×3的矩形块的九个数(如图所示),这九个数的和是中间数的9倍,其中正确的是_____(把所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
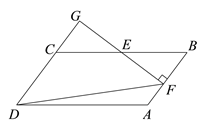
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五四”青年节期间,校团委对团员参加活动情况进行表彰,计划分为优秀奖和贡献奖,为此联系印刷公司设计了两种奖状,A,B两家公司都为学校提出了相同规格和单价的两种奖状,其中优秀奖的奖状6元/张,贡献奖的奖状5元/张,经过协商,A公司的优惠条件是:两种奖状都打八折,但要收制版费50元;B公司的优惠条件是:两种奖状都打九折;根据学校要求,优秀奖的个数是贡献奖的2倍还多10个,如果设贡献奖的个数是x个.
(1)分别写出校团委购买A,B两家印刷厂所需要的总费用y1(元)和y2(元)与贡献奖个数x之间的函数关系式;
(2)校团委选择哪家印刷公司比较合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图.

(1)求y与x之间的函数表达式;
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若原有码头工人10名,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com