
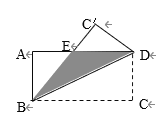
【题目】如图,矩形ABCD中,AB=3,BC=4,将该矩形沿对角线BD折叠,则图中阴影部分的面积是多少?
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
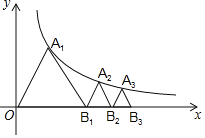
【题目】如图已知等边![]() ,顶点
,顶点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 的坐标为
的坐标为![]() .过
.过![]() 作
作![]() 交双曲线于点
交双曲线于点![]() ,过
,过![]() 作
作![]() 交x轴于点
交x轴于点![]() 得到第二个等边
得到第二个等边![]() ;过
;过![]() 作
作![]() 交双曲线于点
交双曲线于点![]() ,过
,过![]() 作
作![]() 交x轴于点
交x轴于点![]() ,得到第三个等边
,得到第三个等边![]() ;以此类推,…,则点
;以此类推,…,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.
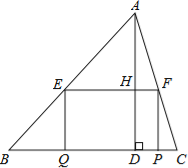
(1)求证:![]() ;
;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求出最大面积;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线DA匀速向上运动(当矩形的边PQ到达A点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
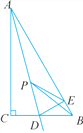
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=60°,D是BC边上的点,CD=1,将△ACD沿直线AD翻折,点C刚好落在AB边上的点E处.若P是直线AD上的动点,则△PEB的周长的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箱子里有4瓶牛奶,其中有一瓶是过期的.现从这4瓶牛奶中任意抽取牛奶饮用,抽取任意一瓶都是等可能的.
(1)若小芳任意抽取1瓶,抽到过期的一瓶的概率是 ;
(2)若小芳任意抽取2瓶,请用画树状图或列表法求,抽出的2瓶牛奶中恰好抽到过期牛奶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑球和白球,这些球除颜色外无其他差别,现让学生进行摸球试验:每次摸出一个球,记下颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 38 | 79 | 121 | 196 | 322 | 398 |
摸到黑棋的频率 | 0.380 | 0.395 | 0.403 | 0.392 | 0.403 | 0.398 |
(1)根据表中数据估计,从盒中摸出一个球是白球的概率是_____(精确到0.01);
(2)若盒中黑球与白球共有5枚,某同学连续不放回地摸出两个球,用树状图或表格计算这两个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开的桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上的数据求出DE的长度.(结果保留根号)
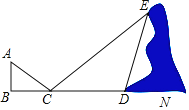
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为48cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于74cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于68cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
(3)该怎么剪,才能使这两个正方形的面积之和为最小,最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com