
【题目】如图Rt△ABC,AB=CB,将△ABC绕A点旋转的度数为a(45°<a<180°),连接BD交AC于F,AH平分∠CAD交BD于点H,若△FHA为等腰三角形,则a=______.

【答案】135°或157.5°
【解析】
根据等腰直角三角形的性质得到∠BAC=45°,根据旋转的性质得到∠BAD=α,AB=AD,求得![]() ,根据角平分线的定义得到
,根据角平分线的定义得到![]() ,根据等腰三角形的性质得到
,根据等腰三角形的性质得到![]() ,求得
,求得![]() ,根据三角形的内角和列方程即可得到结论.
,根据三角形的内角和列方程即可得到结论.
∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵将△ABC绕A点旋转的度数为a得到△ADE,
∴∠BAD=α,AB=AD,
∴![]() ,
,
∵AH平分∠CAD交BD于点H,
∴![]() ,
,
∵AB=AD,
∴![]() ,
,
∴![]() ,
,
若△FHA为等腰三角形,
①当AF=AH,
∴![]() ,
,
∵∠FAH+∠AFH+∠AHF=180°,
∴![]() ,
,
解得:α=135°,
②当AF=FH时,
∴![]() ,
,
∵∠FAH+∠AFH+∠AHF=180°,
∴![]() ,
,
解得:α=180°,(不合题意,舍去);
③当AH=HF时,
∴∠HAF=∠HFA,
∴![]() ,
,
解得:![]() ,
,
综上所述,△FHA为等腰三角形,则a=135°或![]() ,
,
故答案为:135°或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,AD是⊙O的切线,BD∥AC,BD交⊙O于点E,连接AE,则下列结论:①∠DAE=∠BAC;②AE=BE;③AD=AE;④四边形ACBD是平行四边形,其中不正确的是__________.(只填序号)
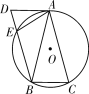
查看答案和解析>>
科目:初中数学 来源: 题型:
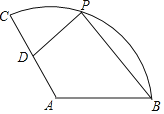
【题目】如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为弧BC上一动点(不与C,B重合),则2PD+PB的最小值为( )
A. ![]() B.
B. ![]() C. 10 D.
C. 10 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,
(1)证明:CF=EB.
(2)证明:AB=AF+2EB.
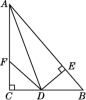
查看答案和解析>>
科目:初中数学 来源: 题型:
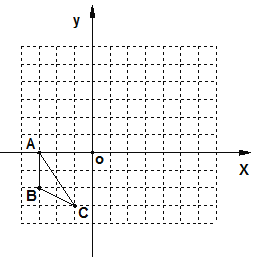
【题目】如图,在边长为1的正方形网格内有一个三角形ABC
(1)把△ABC沿着![]() 轴向右平移5个单位得到△A1B1C1,请你画出△A1B1C1
轴向右平移5个单位得到△A1B1C1,请你画出△A1B1C1
(2)请你以O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2,使得△ABC与△A2B2C2的位似比为1:2;
(3)请你写出△A2B2C2三个顶点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
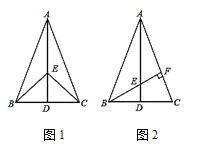
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,∠BAC=45°,原题设其他条件不变.求证:AB=BF+EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形,要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得![]() ,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.
,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.
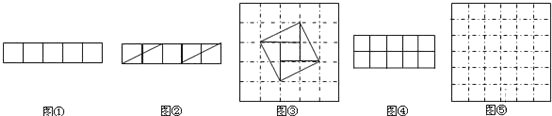
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图④,请把它们分割后拼接成一个新的正方形,要求:在图④中画出分割线,并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.(说明:直接画出图形,不要求写分析过程.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com