
 如图,矩形ABCD中,AB=9,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过2秒时,直线MN和正方形AEFG开始有公共点.
如图,矩形ABCD中,AB=9,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过2秒时,直线MN和正方形AEFG开始有公共点. 分析 首先过点F作FQ⊥CD于点Q,证明△ADE≌△EQF,进而得出AD=EQ,得出当直线MN和正方形AEFG开始有公共点时:DQ+CM≥9,进而求出即可.
解答 解:过点F作FQ⊥CD于点Q,则∠FQE=90°,如图所示:
∵四边形ABCD为矩形,
∴∠D=90°,
∴∠D=∠FQE,
∵在正方形AEFG中,∠AEF=90°,AE=EF,
∴∠AED+∠QEF=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠QEF,
在△ADE和△EQF中,
$\left\{\begin{array}{l}{∠D=∠FQE}\\{∠DAE=∠QEF}\\{AE=EF}\end{array}\right.$,
∴△ADE≌△EQF(AAS),
∴AD=EQ=3,
当直线MN和正方形AEFG开始有公共点时:DQ+CM≥9,
设当经过t秒时,直线MN和正方形AEFG开始有公共点,
则t+3+2t≥9,
解得:t≥2,
故答案为:2.
点评 此题主要考查了正方形的性质、矩形的性质、全等三角形的判定与性质等知识;根据已知得出DQ+CM≥9是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
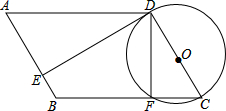 如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边相交于点E,且AE=3EB.
如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边相交于点E,且AE=3EB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
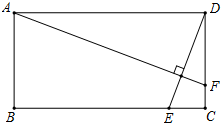 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )
如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 据国家教育部、卫生部最新调查表明:我国小学生近视率超过25%,初中生近视率达到70%,每年以8%的速度增长,居世界第一位.某市为调查中学生视力情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成统计表和扇形统计图如下:
据国家教育部、卫生部最新调查表明:我国小学生近视率超过25%,初中生近视率达到70%,每年以8%的速度增长,居世界第一位.某市为调查中学生视力情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成统计表和扇形统计图如下:| 年份 | 2014 | 2015 | 2016 |
| 人数 | 300 | 500 | 800 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.
已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com