
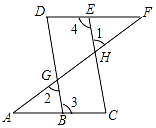
 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F 分析 先证明BD∥CE,得出同旁内角互补∠3+∠C=180°,再由已知得出∠4+∠C=180°,证出 AC∥DF,即可得出结论.
解答 解:∵∠1=∠2(已知)
∠2=∠DGF (对顶角相等)
∴∠1=∠DGF( 等量代换 )
∴BD∥CE (同位角相等,两直线平行)
∴∠3+∠C=180° (两直线平行,同旁内角互补)
又∵∠3=∠4(已知)
∴∠4+∠C=180°
∴AC∥DF∥(同旁内角互补,两直线平行)
∴∠A=∠F (两直线平行,内错角相等);
故答案为:对顶角相等;∠DGF;同位角相等,两直线平行;两直线平行,同旁内角互补;AC,DF;两直线平行,内错角相等.
点评 本题考查了平行线的判定与性质、对顶角相等的性质;熟练掌握平行线的判定与性质是解决问题的关键,注意两者的区别.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
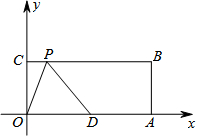 已知,如图:在平面直角坐标系中,O为坐标原点,OABC是长方形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,△ODP是腰长为10的等腰三角形时,求满足条件的点P点坐标.
已知,如图:在平面直角坐标系中,O为坐标原点,OABC是长方形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,△ODP是腰长为10的等腰三角形时,求满足条件的点P点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
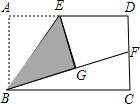 (1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
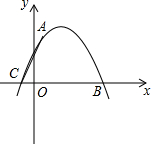 如图,二次函数y=ax2+bx+c的图象经过点A(1,4)与B(5,0),C(-1,0).
如图,二次函数y=ax2+bx+c的图象经过点A(1,4)与B(5,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com