
【题目】如图,![]() 是⊙
是⊙![]() 的直径,弦
的直径,弦![]()
![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接DF.
,连接DF.
(1)求证:DF是⊙![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() =30°,
=30°,![]() ,求
,求![]() 的长.
的长.
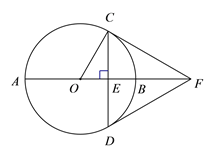
【答案】(1)见解析;(2)![]()
【解析】(1) 连接OD,由垂径定理证OF为CD的垂直平分线,得CF=DF,∠CDF=∠DCF,由∠CDO=∠OCD,再证∠CDO +∠CDB=∠OCD+∠DCF=90°,可得OD⊥DF,结论成立.
(2) 由∠OCF=90°, ∠BCF=30°,得∠OCB=60°,再证ΔOCB为等边三角形,得∠COB=60°,可得∠CFO=30°,所以FO=2OC=2OB,FB=OB= OC =2,在直角三角形OCE中,解直角三角形可得CE,再推出CD=2CE.
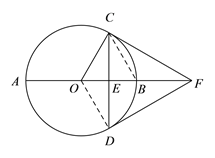
(1)证明:连接OD
∵CF是⊙O的切线
∴∠OCF=90°
∴∠OCD+∠DCF=90°
∵直径AB⊥弦CD
∴CE=ED,即OF为CD的垂直平分线
∴CF=DF
∴∠CDF=∠DCF
∵OC=OD,
∴∠CDO=∠OCD
∴∠CDO +∠CDB=∠OCD+∠DCF=90°
∴OD⊥DF
∴DF是⊙O的切线
(2)解:连接OD
∵∠OCF=90°, ∠BCF=30°
∴∠OCB=60°
∵OC=OB
∴ΔOCB为等边三角形,
∴∠COB=60°
∴∠CFO=30°
∴FO=2OC=2OB
∴FB=OB= OC =2
在直角三角形OCE中,∠CEO=90°∠COE=60°
![]()
∴CF![]()
∴CD=2 CF![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
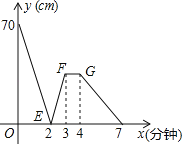
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,经过7min同时到达C点,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 m,甲机器人前2min的速度为 m/min.
(2)若前3min甲机器人的速度不变,求出前3min,甲、乙两机器人之间的距离y(m)与他们的行走时间r(min)之间的关系式.
(3)求出两机器人出发多长时间相距28m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解本校七年级学生课后延时服务课外阅读情况,随机抽取该校七年级部分学生进行问卷调查(每人只选一种书籍),如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
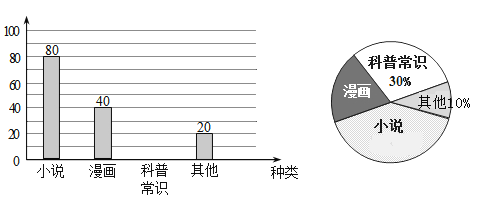
(1)这次活动一共调查了________名学生;
(2)在扇形统计图中,“小说”所在扇形的圆心角等于________;
(3)补全条形统计图.
(4)若该校七年级学生720人,试求出该年级阅读漫画的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从八、九两个年级各随机抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
八年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
九年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按如下分数段整理、描述这两组样本数据:
|
|
|
|
|
| |
八年级 | 0 | 0 | 1 | 11 | 1 | |
九年级 | 1 | 0 | 0 | 7 |
(说明:成绩![]() 分及以上为体质健康优秀,
分及以上为体质健康优秀,![]() ~
~![]() 分为体质健康良好,
分为体质健康良好,![]() ~
~![]() 分为体质健康合格,
分为体质健康合格,![]() 分以下为体质健康不合格)
分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 |
|
|
| 33.6 |
九年级 |
|
| 52.1 |
请将以上两个表格补充完整;
得出结论
(1)估计九年级体质健康优秀的学生人数为__________;
(2)可以推断出_______年级学生的体质健康情况更好一些,理由为_________________.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).
(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在![]() 的条件下,当
的条件下,当![]() 时,n的取值范围是
时,n的取值范围是![]() ,求抛物线的表达式;
,求抛物线的表达式;
②若D点坐标(4,0),当![]() 时,求a的取值范围.
时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意三点A、B、C我们给出如下定义:“横长”a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.
中,对于任意三点A、B、C我们给出如下定义:“横长”a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.
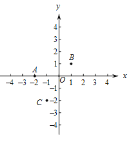
例如:点![]() (
(![]() ,0) ,点
,0) ,点 ![]() (1,1) ,点
(1,1) ,点 ![]() (
(![]() ,
, ![]() ),则
),则![]() 、
、![]() 、
、![]() 三点的 “横长”
三点的 “横长”![]() =|
=|![]() |=3,
|=3,![]() 、
、![]() 、
、![]() 三点的“纵长”
三点的“纵长”![]() =|
=|![]() |=3. 因为
|=3. 因为![]() =
=![]() ,所以
,所以![]() 、
、![]() 、
、![]() 三点为正方点.
三点为正方点.
(1)在点![]() (3,5) ,
(3,5) ,![]() (3,
(3,![]() ) ,
) ,![]() (
(![]() ,
,![]() )中,与点
)中,与点![]() 、
、![]() 为正方点的是 ;
为正方点的是 ;
(2)点P (0,t)为![]() 轴上一动点,若
轴上一动点,若![]() ,
,![]() ,
,![]() 三点为正方点,
三点为正方点,![]() 的值为 ;
的值为 ;
(3)已知点![]() (1,0).
(1,0).
①平面直角坐标系中的点![]() 满足以下条件:点
满足以下条件:点![]() ,
,![]() ,
,![]() 三点为正方点,在图中画出所有符合条件的点
三点为正方点,在图中画出所有符合条件的点![]() 组成的图形;
组成的图形;
②若直线![]() :
:![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 三点为正方点,直接写出m的取值范围.
三点为正方点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在平面直角坐标系中,抛物线y=x![]() +5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
+5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
(1)求点A、B、C的坐标;
(2)求抛物线y=x![]() +5x+4关于坐标原点O对称的抛物线的函数表达式;
+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为![]() ,与x轴交于
,与x轴交于![]() 、
、![]() 两点,与y轴交于
两点,与y轴交于![]() 点,在以A、B、C、M、
点,在以A、B、C、M、![]() 、
、![]() 、
、![]() 、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若分别用x,y(x >y)表示小长方形的长和宽,则下列关系式中不正确的是( )

A. x+y=7 B. x-y=2 C. x2 +y2=25 D. 4xy+4=49
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com