
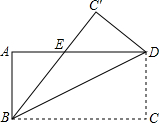
 如图,矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于点E,已知AD=8,AB=4,求△BED的面积.
如图,矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于点E,已知AD=8,AB=4,求△BED的面积. 分析 S△BED=$\frac{1}{2}$DE•AB,所以需求DE的长.根据∠C′BD=∠DBC=∠BDA得DE=BE,设DE=x,则AE=8-x.根据勾股定理求BE即DE的长.
解答 解:∵AD∥BC(矩形的性质),
∴∠DBC=∠BDA(两直线平行,内错角相等);
∵∠C′BD=∠DBC(翻折的性质),
∴∠C′BD=∠BDA(等量代换),
∴DE=BE(等角对等边);
设DE=x,则AE=8-x.
在Rt△ABE中,x2=42+(8-x)2.
解得x=5.
∴S△DBE=$\frac{1}{2}$×5×4=10.
点评 此题通过折叠变换考查了三角形的有关知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后对应边、角相等.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量P(件) | 500 | 490 | 480 | 470 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ
如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com