
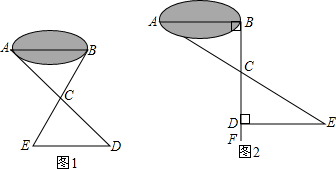
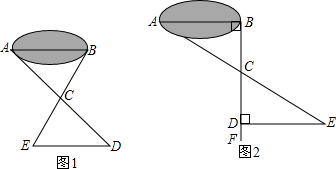
如图所示,为在池塘两侧A、B两处架桥,要知道无法测量的A、B两点的距离,找一处看得见A、B的点P.

(1)连结AP并延长到D,使PA=PD,连结BP,并延长到C,使PC=PB.测得CD=35m,就确定了AB也是35m,说明其中的理由;
(2)也可先过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD.接着过点D作BD的垂线DE交AC的延长线于E,则测出DE的长即为A、B的距离.你认为这种方案是否切实可行,请说出你的理由.作BD⊥AB,ED⊥BF的目的是什么?若满足∠ABD=∠BDE≠![]() ,此方案是否仍然可行?为什么?
,此方案是否仍然可行?为什么?
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,友芝村有一口呈四边形的池塘,在它的四个角A、B、C、D处均种有一棵大核桃树,该村准备挖池塘建养鱼池,要使建后的鱼池面积为原池塘面积的两倍,又想保证树不动,并要求建后的池塘成平行四边形形状.请问友芝村能否实现这一设想?若能,请你设计并画出图形,若不能,请说明理由(画图保留作图痕迹,不写画法).
如图所示,友芝村有一口呈四边形的池塘,在它的四个角A、B、C、D处均种有一棵大核桃树,该村准备挖池塘建养鱼池,要使建后的鱼池面积为原池塘面积的两倍,又想保证树不动,并要求建后的池塘成平行四边形形状.请问友芝村能否实现这一设想?若能,请你设计并画出图形,若不能,请说明理由(画图保留作图痕迹,不写画法).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:辽宁省期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com