
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,AD+AB=2AE,
求证:∠ADC+∠B=180

【答案】见解析.
【解析】
延长AD过C作CF垂直AD于F,由条件可证△AFC≌△AEC,得到CF=CE.再由条件AD+AB=2AE可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠B=∠FDC,问题得证.
证明:延长AD过C作CF垂直AD于F,
∵AC平分∠BAD,
∴∠FAC=∠EAC,
∵CE⊥AB,CF⊥AD,
∴∠AFC=∠AEC=90°,AC=AC,
∴△AFC≌△AEC(AAS),
∴AF=AE,CF=CE,
∵AD+AB=2AE,
又∵AD=AFDF,AB=AE+BE,AF=AE,
∴2AE=AE+BE+AEDF,
∴BE=DF,
在△CDF和△CBE中,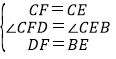 ,
,
∴△CDF≌△CBE(SAS),
∴∠B=∠FDC,
∵∠ADC+∠FDC=180°,
∴∠ADC+∠B=180.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
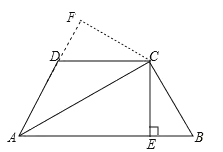
【题目】如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:FE是⊙O的切线;
(2)若FE=4,FC=2,求⊙O的半径及CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段![]()
(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向点
向点![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 沿线段点
沿线段点![]() 向点
向点![]() 以
以![]() 的速度运动,几秒钟后,
的速度运动,几秒钟后,![]() 两点相遇?
两点相遇?
(2)如图1,几秒后,点![]() 两点相距
两点相距![]() ?
?
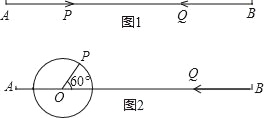
(3)如图2,![]() ,
,![]() ,当点
,当点![]() 在
在![]() 的上方,且
的上方,且![]() 时,点
时,点![]() 绕着点
绕着点![]() 以30度/秒的速度在圆周上逆时针旋转一周停止,同时点
以30度/秒的速度在圆周上逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 两点能相遇,求点
两点能相遇,求点![]() 的运动速度.
的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆![]() 的高度.先在教学楼的底端
的高度.先在教学楼的底端![]() 点处,观测到旗杆顶端
点处,观测到旗杆顶端![]() 得
得![]() ,然后爬到教学楼上的
,然后爬到教学楼上的![]() 处,观测到旗杆底端
处,观测到旗杆底端![]() 的俯角是
的俯角是![]() .已知教学楼中
.已知教学楼中![]() 、
、![]() 两处高度为
两处高度为![]() 米.
米.
(1)求教学楼与旗杆的水平距离![]() ;(结果保留根号);
;(结果保留根号);
(2)求旗杆![]() 的高度.
的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,b)是抛物线![]() 上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )
上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )
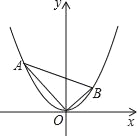
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生会倡导的“爱心捐款”活动结束后,学生会干部对捐款情况作了抽样调查,并绘制了统计图,图中从左到右各长方形高度之比为![]() ,又知此次调查中捐15元和20元的人数共26人.
,又知此次调查中捐15元和20元的人数共26人.
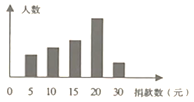
(1)他们一共抽查了______人;
(2)抽查的这些学生,总共捐款______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图①,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
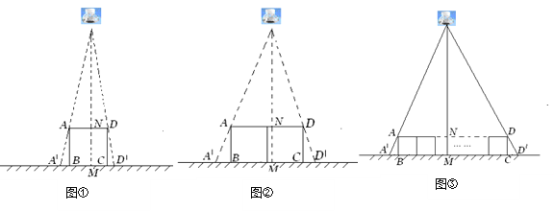 (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图③摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com