
| A. | -1 | B. | 27 | C. | 9 | D. | 3 |
分析 把已知条件整理得:(a-$\frac{1}{3}$)2+(b+3)2=0,根据非负数的性质即可解决问题.
解答 解:∵a2+b2=$\frac{2}{3}a-6b-\frac{82}{9}$,
∴(a2-$\frac{2}{3}$a+$\frac{1}{9}$)+(b2+6b+9)=0,
∴(a-$\frac{1}{3}$)2+(b+3)2=0,
∵(a-$\frac{1}{3}$)2≥0,(b+3)2≥0,
∴a=$\frac{1}{3}$,b=-3,
∴ab=($\frac{1}{3}$)-3=27,
故选B.
点评 本题考查因式分解的应用、非负数的性质,负指数幂等知识,解题的关键是灵活运用配方法因式分解,学会利用非负数的性质解决实际问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
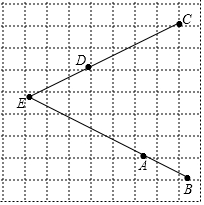 如图,在每个小正方形的边长为1的网格中,A,B为小正方形边的中点,C,D为格点,E为BA,CD的延长线的交点.
如图,在每个小正方形的边长为1的网格中,A,B为小正方形边的中点,C,D为格点,E为BA,CD的延长线的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
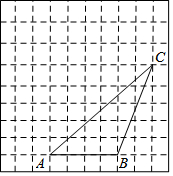 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 数量x(千克) | 1 | 2 | 3 | 4 | … |
| 售价y(元) | 8+0.4 | 16+0.8 | 24+1.2 | 32+1.6 | … |
| A. | y=8+0.4x | B. | y=8x+0.4 | C. | y=8.4x | D. | y=8.4x+0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
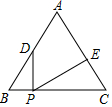 如图,在等边三角形ABC中,BC=8,点D是边AB上一点,且BD=3,点P是边BC上一动点,作∠DPE=60°,PE交边AC于点E,当CE=$\frac{16}{3}$时,满足条件的点P有且只有一个.
如图,在等边三角形ABC中,BC=8,点D是边AB上一点,且BD=3,点P是边BC上一动点,作∠DPE=60°,PE交边AC于点E,当CE=$\frac{16}{3}$时,满足条件的点P有且只有一个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com