
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 找出二次函数与x轴的交点,结合点P所在的象限分段考虑,再根据二次函数的性质找出其最值以及在各段区间内的增减性,对比4个结论即可得知正确的结论有两个.
解答 解:令二次函数y=x2-2x-3中y=0,即x2-2x-3=0,
解得:x1=-1,x2=3.
(i)当x≤-1时,d1=x2-2x-3,d2=-x,
d=d1+d2=x2-3x-3=$(x-\frac{3}{2})^{2}-\frac{21}{4}$,
d≥1;
(ii)当-1<x≤0时,d1=-x2+2x+3,d2=-x,
d=-x2+x+3=-$(x-\frac{1}{2})^{2}+\frac{13}{4}$,
1<d≤3;
(iii)当0<x≤3时,d1=-x2+2x+3,d2=x,
d=-x2+3x+3=-$(x-\frac{3}{2})^{2}$+$\frac{21}{4}$,
3≤d≤$\frac{21}{4}$;
(iv)当3<x时,d1=x2-2x-3,d2=x,
d=d1+d2=x2-x-3=$(x-\frac{1}{2})^{2}-\frac{13}{4}$,
3<d.
综上可知:d有最小值,没有最大值,即①成立,②不成立;
当0<x≤$\frac{3}{2}$时,d随x的增大而增大,$\frac{3}{2}$<x≤3时,d随x的增大而减小,
∴-1<x<3时,d随x的增大而增大,结论③不成立;
令d=5,(i)中存在一个解;(ii)中无解;(iii)中有两个解;(iv)中一个解.
∴满足d=5的点P有四个,结论④成立.
∴正确的结论有2个.
故选B.
点评 本题考查了二次函数的性质,解题的关键是根据点P所在的区间进行分段.本题属于基础题,难度不大,解决该题型题目时,根据二次函数的性质找出函数在各段区间内的增减性与最值是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
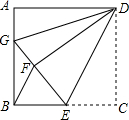 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
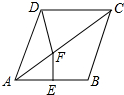 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )| A. | 86° | B. | 76° | C. | 66° | D. | 52° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
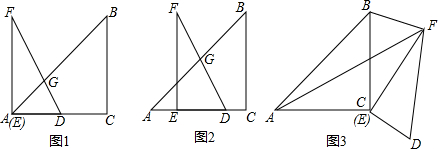
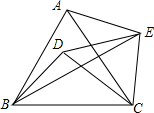 如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
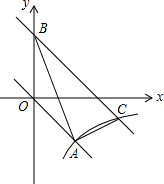 如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).
如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com