
| A. | 在足球赛中,弱队战胜强队 | |
| B. | 长分别为3、5、9厘米的三条线段能围成一个三角形 | |
| C. | 抛掷一枚硬币,落地后正面朝上 | |
| D. | 任取两个正整数,其和大于1 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
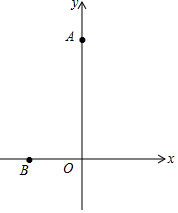 如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明打算用一个45°的三角板和一把带刻度的直尺测量一个圆盘的半径,先将圆盘贴在墙拐角的边沿上,然后将直尺靠在圆盘的下方,直尺的0刻度一端和墙靠在一起,再将45°的三角板的直角边和直尺靠在一起,三角板的斜边和圆盘靠在一起,试通过图中数据求出圆的半径.(精确到0.1)
如图,小明打算用一个45°的三角板和一把带刻度的直尺测量一个圆盘的半径,先将圆盘贴在墙拐角的边沿上,然后将直尺靠在圆盘的下方,直尺的0刻度一端和墙靠在一起,再将45°的三角板的直角边和直尺靠在一起,三角板的斜边和圆盘靠在一起,试通过图中数据求出圆的半径.(精确到0.1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com