
分析 ①原式利用绝对值的代数意义化简,计算即可得到结果;
②原式先计算乘除运算,再计算加减运算即可得到结果;
③原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
④原式逆用积的乘方运算法则变形,计算即可得到结果;
⑤原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
⑥原式先计算乘法运算,再计算加减运算即可得到结果;
⑦原式利用拆项法变形后,计算即可得到结果;
⑧原式提取公因式,计算即可得到结果.
解答 解:①原式=3$\frac{7}{8}$-8+3$\frac{1}{2}$=7$\frac{3}{8}$-8=-$\frac{5}{8}$;
②原式=-$\frac{19}{7}$+$\frac{6}{7}$-$\frac{15}{7}$=-4;
③原式=-4+3+2=1;
④原式=(-2)×(2×0.5)2009+(-7+$\frac{1}{14}$)×7=-2-49+$\frac{1}{2}$=-50$\frac{1}{2}$;
⑤原式=-1-(1$\frac{3}{7}$-2)2×(-$\frac{27}{64}$)=-1-$\frac{16}{49}$×(-$\frac{27}{64}$)=-1+$\frac{27}{196}$=-$\frac{169}{196}$;
⑥原式=(3.95-1.45)×6-(14-15+7)=15-14+15-7=9;
⑦原式=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{1997}$-$\frac{1}{1999}$)=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{1999}$)=$\frac{998}{5997}$;
⑧原式=(-2)2015×(1-2)=22015.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
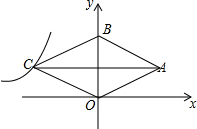 菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )| A. | 12 | B. | 24 | C. | -12 | D. | -24 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
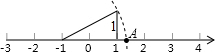 如图所示,数轴上点A所表示的数为a,则a的值是( )
如图所示,数轴上点A所表示的数为a,则a的值是( )| A. | -$\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | $\sqrt{5}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
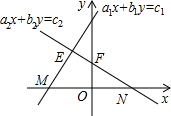 如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解,那么这个点是( )
如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解,那么这个点是( )| A. | M | B. | N | C. | E | D. | F |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 2 | 4 | 2 | 1 |
| A. | 平均数是20.5 | B. | 众数是4 | ||
| C. | 中位数是40 | D. | 这10户家庭月用电量共205度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由①得x=$\frac{2-4y}{3}$ | B. | 由①得y=$\frac{2-3x}{4}$ | C. | 由②得x=$\frac{5+y}{2}$ | D. | 由②得y=2x-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com