
【题目】如图,已知△ABC,点D、E分别在边AC、AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是( )

A. AE=AD;B. BD=CE;C. ∠ECB=∠DBC ;D. ∠BEC=∠CDB.
【答案】D
【解析】
添加AE=AD、BD=CE、∠ECB=∠DBC可利用AAS判定△ABD≌△ACE,进而可得AB=AC,从而可得△ABC是等腰三角形;添加∠BEC=∠CDB不能判定△ABD≌△ACE,因此也不能证明AB=AC,进而不能证明△ABC是等腰三角形.
A、添加AE=AD,
在△ABD和△ACE中
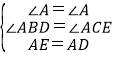 ,
,
∴△ABD≌△ACE(AAS),
∴AB=AC,
∴△ABC为等腰三角形,故此选项不合题意;
B、添加BD=CE,
在△ABD和△ACE中
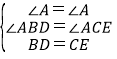 ,
,
∴△ABD≌△ACE(AAS),
∴AB=AC,
∴△ABC为等腰三角形,故此选项不合题意;
C、添加∠ECB=∠DBC,
又∵∠ABD=∠ACE,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC为等腰三角形,故此选项不合题意;
D、添加∠BEC=∠CDB,不能证明△ABD≌△ACE,因此也不能证明AB=AC,进而得不到△ABC为等腰三角形,故此选项符合题意;
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,按以下步骤作图:
,按以下步骤作图:
①:以点![]() 为圆心,以小于
为圆心,以小于![]() 的长为半径画弧,分别交
的长为半径画弧,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;
;
②:分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧相交于点
的长为半径画弧,两弧相交于点![]() ;
;
③:作射线![]() ,交
,交![]() 边于点
边于点![]() ,
,
若![]() ,
,![]() ,则
,则![]() ( )
( )
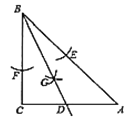
A. 3B. ![]() C. 6D.
C. 6D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
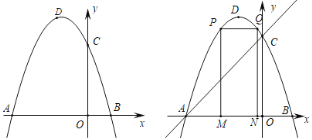
【题目】如图,抛物线的图象与x轴交A(-3,0),B(1,0)两点,与y轴交于点C(0,3),点D为抛物线的顶点.
(1)求抛物线的解析式;
(2)设点T在第二象限的抛物线上,若其关于原点的对称点也在抛物线上,求点T的坐标;
(3)点M为线段AB上一点(点M不与点A,B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
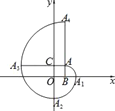
【题目】如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),弧AA1是以点B为圆心,BA为半径的圆弧;弧A1A2是以点O为圆心,OA2为半径的圆弧;弧A2A3是以点C为圆心,CA2为半径的圆弧;弧A3A4是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心,按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,则点A2019的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD,点E在边AD上,AF⊥BE,垂足为点F,点G在线段BF上,BG=AF.
(1)求证:CG⊥BE;
(2)如果点E是AD的中点,联结CF,求证:CF=CB.

查看答案和解析>>
科目:初中数学 来源: 题型:
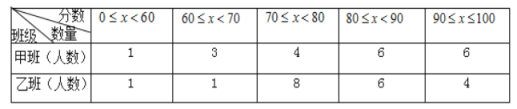
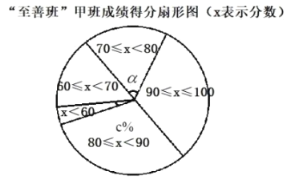
【题目】某中学初三年级积极推进走班制教学。为了了解一段时间以来,“至善班”的学习效果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取![]() 名同学在某一次定时测试中的数学成绩,其结果记录如下:
名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班的![]() 名同学的数学成绩统计(满分为
名同学的数学成绩统计(满分为![]() 分) (单位:分)
分) (单位:分)

“至善班”甲=乙班的![]() 名同学的数学成绩统计(满分为
名同学的数学成绩统计(满分为![]() 分) (单位:分)
分) (单位:分)

整理数据:(成绩得分用![]() 表示)
表示)
分析数据,并回答下列问题:
![]() 完成下表:
完成下表:
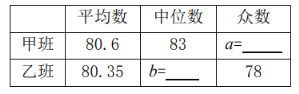
![]() 在“至善班”甲班的扇形图中,成绩在
在“至善班”甲班的扇形图中,成绩在![]() 的扇形中,说对的圆心角
的扇形中,说对的圆心角![]() 的度数为 .估计全部“至善班”的
的度数为 .估计全部“至善班”的![]() 人中优秀人数为 人.(
人中优秀人数为 人.(![]() 分及以上为优秀).
分及以上为优秀).
![]() 根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:
根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:
① .
② .
查看答案和解析>>
科目:初中数学 来源: 题型:
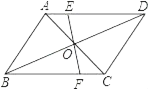
【题目】如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com