
【题目】期中考试临近,某校初二年级教师对复习课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
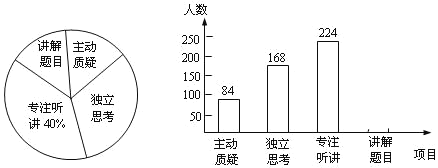
(1)在这次评价中,一共抽查了_________名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为______度;
(3)请将频数分布直方图补充完整;
(4)如果全市有8000名初二学生,那么在复习课中,“独立思考”的学生约有多少人?
【答案】(1)560,(2) 54°(3) 见解析(4)2400
【解析】
(1)由“专注听讲”的学生人数除以占的百分比求出调查学生总数即可;
(2)由“主动质疑”占的百分比乘以360°即可得到结果;
(3)求出“讲解题目”的学生数,补全统计图即可;
(4)求出“独立思考”学生占的百分比,乘以8000即可得到结果.
解:(1)根据题意得:224÷40%=560(名),
则在这次评价中,一个调查了560名学生;
故答案为:560;
(2)根据题意得:![]() ×360°=54°,
×360°=54°,
则在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为54度;
故答案为:54;
(3)“讲解题目”的人数为560﹣(84+168+224)=84,补全统计图如下:
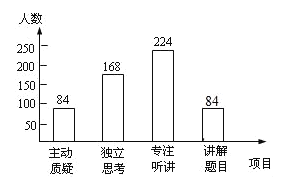
(4)根据题意得:8000×![]() ×100%=2400(人),
×100%=2400(人),
则“独立思考”的学生约有2400人.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】定义新运算:![]() .
.
例如:3![]() 2=3(3-2)=3,-1
2=3(3-2)=3,-1![]() 4=-1
4=-1![]() (-1-4)=5.
(-1-4)=5.
(1)请直接写出3![]() a=b的所有正整数解;
a=b的所有正整数解;
(2)已知2![]() a=5b-2m,3
a=5b-2m,3![]() b=5a+m,说明:12a+11b的值与m无关;
b=5a+m,说明:12a+11b的值与m无关;
(3)已知a>1,记M=ab![]() b,N=b
b,N=b![]() ab,试比较M,N的大小.
ab,试比较M,N的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=![]() OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC于点F.
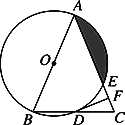
(1)判断DF与是⊙O的位置关系,并证明你的结论。
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
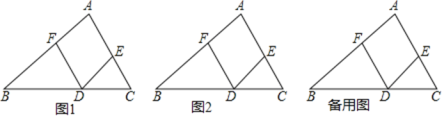
【题目】已知:如图1,DE∥AB,DF∥AC.
(1)求证:∠A=∠EDF.
(2)点G是线段AC上的一点,连接FG,DG.
①若点G是线段AE的中点,请你在图2中补全图形,判断∠AFG,∠EDG,∠DGF之间的数量关系,并证明.
②若点G是线段EC上的一点,请你直接写出∠AFG,∠EDG,∠DGF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为应对越来越复杂的交通状况,某城市对其道路进行拓宽改造,工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了拓宽改造任务.下面能反映该工程尚未改造的道路![]() (米)与时间
(米)与时间![]() (天)的关系的大致图象是( )
(天)的关系的大致图象是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)参与问卷调查的总人数为 ,扇形统计图中“B”对应的扇形的圆心角度数等于 °;
(2)补全条形统计图.
(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com