
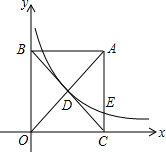
 如图,已知矩形ABOC的对角线相交于点D,O为坐标原点,OC在x轴的正半轴上,双曲线y=$\frac{k}{x}$(k>0)经过点D,与边AC相交于点E.若OC2=CE•CA,则直线OA的解析式为y=2x.
如图,已知矩形ABOC的对角线相交于点D,O为坐标原点,OC在x轴的正半轴上,双曲线y=$\frac{k}{x}$(k>0)经过点D,与边AC相交于点E.若OC2=CE•CA,则直线OA的解析式为y=2x. 分析 过D作DF⊥OC于F,设D(m,$\frac{k}{m}$),则E(2m,$\frac{k}{2m}$),A(2m,$\frac{2k}{m}$),利用OC2=CE•CA,求出k、m关系,得到点D坐标(m,2m),再利用待定系数法确定直线OA解析式即可.
解答 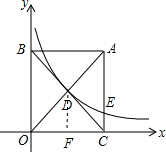 解:过D作DF⊥OC于F,
解:过D作DF⊥OC于F,
∵四边形ABOC是矩形,
∴AD=OD=CD,DF∥AC,
∴OC=2OF,
设D(m,$\frac{k}{m}$),
∴AC=$\frac{2k}{m}$,OC=2m,
∵E在双曲线y=$\frac{k}{x}$(k>0)上,
∴E(2m,$\frac{k}{2m}$),A(2m,$\frac{2k}{m}$),
∴CE=$\frac{k}{2m}$,
∵OC2=CE•CA,
∴4m2=$\frac{k}{2m}$•$\frac{2k}{m}$,
∴k=2m2,
∴点D坐标(m,2m),
设直线OA为y=kx,则2m=km,
∴k=2,
∴直线OA为:y=2x.
故答案为y=2x.
点评 本题考查矩形的性质、反比例函数的性质等知识,解题的关键是设参数利用已知条件求出参数之间关系,学会待定系数法确定函数解析式,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2x+1}$ | B. | $\frac{1}{2x-1}$ | C. | $\frac{1-3x}{{x}^{2}}$ | D. | $\frac{5x+3}{2{x}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 测量某天的最高气温是100℃ | |
| B. | 度量四边形的内角和,结果是360° | |
| C. | 掷一枚骰子,向上一面的数字是2 | |
| D. | 袋中装有5只黑球,从中摸出一个是黑球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
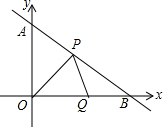 综合与探究:如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.
综合与探究:如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com