
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.

【答案】(1)y=﹣x2+2x+3;(2)①S四边形ACFD= 4;②Q点坐标为(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由A、B两点的坐标,利用待定系数法即可求得抛物线解析式;
(2)①连接CD,则可知CD∥x轴,由A、F的坐标可知F、A到CD的距离,利用三角形面积公式可求得△ACD和△FCD的面积,则可求得四边形ACFD的面积;②由题意可知点A处不可能是直角,则有∠ADQ=90°或∠AQD=90°,当∠ADQ=90°时,可先求得直线AD解析式,则可求出直线DQ解析式,联立直线DQ和抛物线解析式则可求得Q点坐标;当∠AQD=90°时,设Q(t,-t2+2t+3),设直线AQ的解析式为y=k1x+b1,则可用t表示出k′,设直线DQ解析式为y=k2x+b2,同理可表示出k2,由AQ⊥DQ则可得到关于t的方程,可求得t的值,即可求得Q点坐标.
(1)由题意可得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴F(1,4),
∵C(0,3),D(2,3),
∴CD=2,且CD∥x轴,
∵A(﹣1,0),
∴S四边形ACFD=S△ACD+S△FCD=![]() ×2×3+
×2×3+![]() ×2×(4﹣3)=4;
×2×(4﹣3)=4;
②∵点P在线段AB上,
∴∠DAQ不可能为直角,
∴当△AQD为直角三角形时,有∠ADQ=90°或∠AQD=90°,
i.当∠ADQ=90°时,则DQ⊥AD,
∵A(﹣1,0),D(2,3),
∴直线AD解析式为y=x+1,
∴可设直线DQ解析式为y=﹣x+b′,
把D(2,3)代入可求得b′=5,
∴直线DQ解析式为y=﹣x+5,
联立直线DQ和抛物线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴Q(1,4);
ii.当∠AQD=90°时,设Q(t,﹣t2+2t+3),
设直线AQ的解析式为y=k1x+b1,
把A、Q坐标代入可得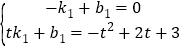 ,解得k1=﹣(t﹣3),
,解得k1=﹣(t﹣3),
设直线DQ解析式为y=k2x+b2,同理可求得k2=﹣t,
∵AQ⊥DQ,
∴k1k2=﹣1,即t(t﹣3)=﹣1,解得t=![]() ,
,
当t=![]() 时,﹣t2+2t+3=
时,﹣t2+2t+3=![]() ,
,
当t=![]() 时,﹣t2+2t+3=
时,﹣t2+2t+3=![]() ,
,
∴Q点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上可知Q点坐标为(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
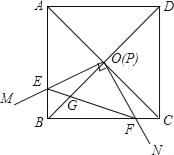
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是_____.
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(4)OGBD=AE2+CF2.
;(4)OGBD=AE2+CF2.
查看答案和解析>>
科目:初中数学 来源: 题型:
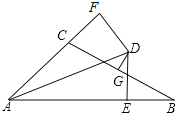
【题目】已知∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,
(1)连接CD、BD,求证:△CDF≌△BDE;
(2)若AE=5,AC=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在ΔABC中,AB=AC,周长为24,AC边上的中线BD把ΔABC分成周长为9和15的两个部分,则ΔABC各边的长分别为( )
A.10、10、4B.6、6、12C.5、9、10D.10、10、4或6、6、12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦今年一月份销售额为![]() 万元,二月份由于种种原因,经营不善,销售额下降
万元,二月份由于种种原因,经营不善,销售额下降![]() ,以后加强改进管理,经减员增效,大大激发了全体员工的积极性,月销售额大幅度上升,到四月份销售额猛增到
,以后加强改进管理,经减员增效,大大激发了全体员工的积极性,月销售额大幅度上升,到四月份销售额猛增到![]() 万元,求三、四月份平均每月增长的百分率是多少?
万元,求三、四月份平均每月增长的百分率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图反映了初三(1)班、(2)班的体育成绩。

(1)不用计算,根据条形统计图,_______班学生的体育成绩好一些。
(2)从图中观察出:三(1)班学生体育成绩等级的众数是_______;三(2)班学生体育成绩等级的众数是_______.
(3)如果依次将不及格、及格、中、良好、优秀记为55、65、75、85、95分,请你观察计算一下初三(1),(2)班的平均成绩各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种成本为![]() 元
元![]() 的水产品,若按
的水产品,若按![]() 元
元![]() 销售,一个月可售出
销售,一个月可售出![]() ,售价毎涨
,售价毎涨![]() 元,月销售量就减少
元,月销售量就减少![]() .
.
![]() 写出月销售利润
写出月销售利润![]() (元)与售价
(元)与售价![]() (元
(元![]() )之间的函数表达式;
)之间的函数表达式;
![]() 当售价定为多少元时,该商店月销售利润为
当售价定为多少元时,该商店月销售利润为![]() 元?
元?
![]() 当售价定为多少元时会获得最大利润?求出最大利润.
当售价定为多少元时会获得最大利润?求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com