
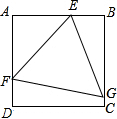
 如图,正△EFG内接于正方形ABCD,其中E,F,G分别在边AB,AD,BC上,若
如图,正△EFG内接于正方形ABCD,其中E,F,G分别在边AB,AD,BC上,若| AE |
| EB |
| BG |
| BC |
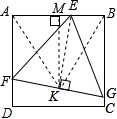 解:如图,作EK⊥FG,K是FG的中点,连AK、KB,易知E、K、G、B和E、K、F、A分别四点共圆
解:如图,作EK⊥FG,K是FG的中点,连AK、KB,易知E、K、G、B和E、K、F、A分别四点共圆| 1 |
| 3 |
| 3 |
| ME2+MK2 |
| 7 |
| EK |
| sin60° |
4
| ||
| 3 |
| EG2-BE2 |
10
| ||
| 3 |
| BG |
| BC |
5
| ||
| 9 |
5
| ||
| 9 |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源:2011年1月浙江省杭州市滨江区九年级(上)月考数学试卷(解析版) 题型:填空题
 如图,正△EFG内接于正方形ABCD,其中E,F,G分别在边AB,AD,BC上,若
如图,正△EFG内接于正方形ABCD,其中E,F,G分别在边AB,AD,BC上,若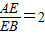 ,则
,则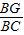 = .
= .查看答案和解析>>
科目:初中数学 来源:2009年数学九年级奥林匹克初中训练(06)(解析版) 题型:填空题
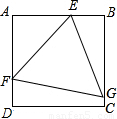 如图,正△EFG内接于正方形ABCD,其中E,F,G分别在边AB,AD,BC上,若
如图,正△EFG内接于正方形ABCD,其中E,F,G分别在边AB,AD,BC上,若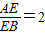 ,则
,则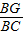 = .
= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com