
【题目】观察发现:如图(1),![]() 是
是![]() 的外接圆,点
的外接圆,点![]() 是边
是边![]() 上的一点,且
上的一点,且![]() 是等边三角形.
是等边三角形.![]() 与
与![]() 交于点
交于点![]() ,以
,以![]() 为圆心、
为圆心、![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)![]() _____;
_____;
(2)线段![]() 、
、![]() 有何大小关系?证明你的猜想.
有何大小关系?证明你的猜想.
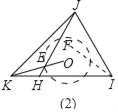
拓展应用:如图(2),![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 延长线上的一点.点
延长线上的一点.点![]() 是
是![]() 的外接圆圆心,
的外接圆圆心,![]() 与
与![]() 相交于点
相交于点![]() .如果等边三角形
.如果等边三角形![]() 的边长为2,请直接写出
的边长为2,请直接写出![]() 的最小值和此时
的最小值和此时![]() 的度数.
的度数.

【答案】(1)120°;(2)见解析;(3)拓展应用:![]() 的最小值为
的最小值为![]() ,此时
,此时![]() .
.
【解析】
(1)根据△ABC是等边三角形,可得∠ACB=60°,根据圆周角定理可得∠AOD的度数.(2)根据内角和定理和等边三角形的性质可得![]() ,进而得到
,进而得到![]() ,根据边角边对应相等可得
,根据边角边对应相等可得![]() ,则
,则![]() .
.
拓展应用:以![]() 为圆心,以
为圆心,以![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() .当
.当![]() 时
时![]() 最小,
最小,![]() 时,
时,![]() .
.
解:观察发现:(1)∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠AOD=2∠ACB=120°
故答案为120°.
(2)结论:AE=CF.
理由如下:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
拓展应用:以![]() 为圆心,以
为圆心,以![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() ,连结
,连结![]() ,则由以上结论可得:
,则由以上结论可得:![]() .
.
当![]() 时
时![]() 最小,
最小,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() ,此时
,此时![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).

(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.
(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
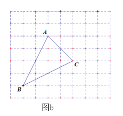
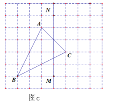
(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
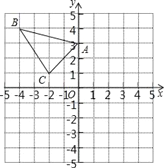
【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其他区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1 000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题 .
已知 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….,当
,….,当![]() 为大于1的奇数时,
为大于1的奇数时,![]() ;当
;当![]() 为大于1的偶数时,
为大于1的偶数时,![]() .
.
(1)求![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(2)直接写出![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(3)计算:![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com