
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时点
移动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,点
的延长线移动,点![]() ,
,![]() 移动的速度相同,
移动的速度相同,![]() 与
与![]() 相交于点
相交于点![]() .
.
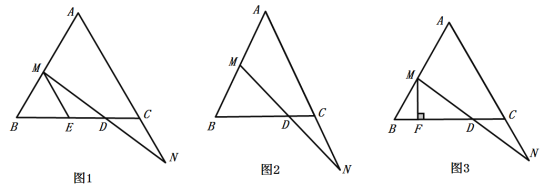
(1)如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() ,当点
,当点![]() 移动到
移动到![]() 的中点时,求
的中点时,求![]() 的长度;
的长度;
(3)如图3,过点![]() 作
作![]() 于点
于点![]() .在点
.在点![]() 从点
从点![]() 向点
向点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)移动的过程中,线段
重合)移动的过程中,线段![]() 与
与![]() 的长度是否保持不变若保持不变,请求出
的长度是否保持不变若保持不变,请求出![]() 与
与![]() 的长度和;若改变,请说明理由.
的长度和;若改变,请说明理由.
【答案】(1)证明见解析;(2)![]() 的长度为
的长度为![]() ;(3)
;(3)![]() 与
与![]() 的长度和保持不变,和为4.
的长度和保持不变,和为4.
【解析】
(1)由平行的性质和等腰三角形的性质进行等边和等角转换,即可判定![]() ;
;
(2)由(1)的结论和等边三角形的性质,通过等量转换即可得解;
(3)首先过点![]() 作
作![]() ,由等腰三角形的性质以及全等三角形的性质,即可求得
,由等腰三角形的性质以及全等三角形的性质,即可求得![]() 与
与![]() 的长度保持不变.
的长度保持不变.
(1)∵点![]() ,
,![]() 同时移动且移动的速度相同,
同时移动且移动的速度相同,
![]() ,
,
![]() ,
,
![]()
又![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 与
与![]() 相交于点
相交于点![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,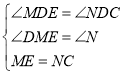 ,
,
![]() (AAS);
(AAS);
(2)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,如图所示:
,如图所示:

![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]()
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() .
.
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() .
.
由(1)易得![]() ,
,
![]() ,
,
![]() ,
,
![]() 的长度为
的长度为![]() ;
;
(3)保持不变;
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,如图所示:
,如图所示:
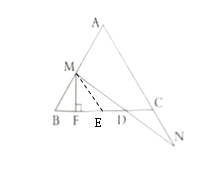
由(1)易得![]() ,
,![]() ,
,
![]() ,
,![]() 是等腰三角形.
是等腰三角形.
![]() ,
,
![]() 是
是![]() 的中线,
的中线,
![]() ,
,
![]() ,
,
![]() 与
与![]() 的长度和保持不变.
的长度和保持不变.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
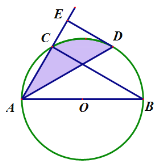
【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AD=BC,⊙O半径为6,求∠CAD与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种成本为每千克![]() 元的水产品,据市场分析,若按每千克
元的水产品,据市场分析,若按每千克![]() 元销售,一个月能售出
元销售,一个月能售出![]() ,销售单价每涨(或跌)
,销售单价每涨(或跌)![]() 元,月销售量就减少(或增加)
元,月销售量就减少(或增加)![]() ,解答以下问题:
,解答以下问题:
(1)当销售单价定位每千克![]() 元时,计算月销售量和月销售利润;
元时,计算月销售量和月销售利润;
(2)商店想在月销售成本不超过![]() 元的情况下,使得月销售利润达到
元的情况下,使得月销售利润达到![]() 元,销售单价应为多少?
元,销售单价应为多少?
(3)商店要使得月销售利润达到最大,销售单价应为多少?此时利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为__________.
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套100平方米的房子,开发商给予以下两种优惠方案供其选择:①打9.8折销售;②不打折,送两年物业管理费.物业管理费每平方米每月1.5元,请问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探BM,MN,CN之间的数量关系,并给出证明.
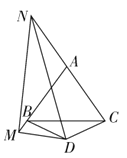
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,结合函数![]() 的图象填空:
的图象填空:![]() 随
随![]() 的增大而___________,当
的增大而___________,当![]() 时,该函数的最大值为_________,最小值为_________.
时,该函数的最大值为_________,最小值为_________.
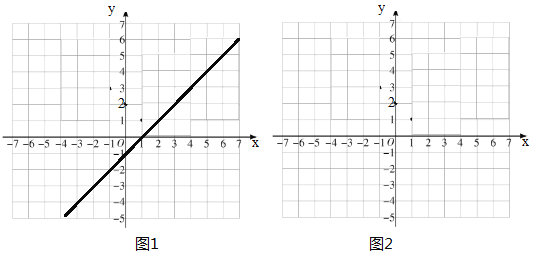
(2)根据学习函数的经验来探究函数![]() 的最小值.
的最小值.
①若点![]() 和点
和点![]() 是该函数图象上的两点,则
是该函数图象上的两点,则![]() _________;
_________;
②在平面直角坐标系中描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;
③由图象可知,函数![]() 的最小值为___________.
的最小值为___________.
(3)请结合![]() 的取值范围判断方程
的取值范围判断方程![]() 的解的个数.(直接写出结果)
的解的个数.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com