
 如图,在矩形ABCD中,AB=8,AD=12,过点A、D两点的⊙O与BC边相切于点E,则⊙O的半径为$\frac{25}{4}$.
如图,在矩形ABCD中,AB=8,AD=12,过点A、D两点的⊙O与BC边相切于点E,则⊙O的半径为$\frac{25}{4}$. 分析 连结EO并延长交AD于F,如图,由切线的性质得OE⊥BC,再利用平行线的性质得到OF⊥AD,则根据垂径定理得到AF=DF=$\frac{1}{2}$AD=6,易得四边形ABEF为矩形,则EF=AB=8,设⊙O的半径为r,则OA=r,OF=8-r,然后在Rt△AOF中利用勾股定理得到(8-r)2+62=r2,再解方程求出r即可.
解答 解: 连结EO并延长交AD于F,如图,
连结EO并延长交AD于F,如图,
∵⊙O与BC边相切于点E,
∴OE⊥BC,
∵四边形ABCD为矩形,
∴BC∥AD,
∴OF⊥AD,
∴AF=DF=$\frac{1}{2}$AD=6,
易得四边形ABEF为矩形,则EF=AB=8,设⊙O的半径为r,则OA=r,OF=8-r,
在Rt△AOF中,∵OF2+AF2=OA2,
∴(8-r)2+62=r2,解得r=$\frac{25}{4}$,
即⊙O的半径为$\frac{25}{4}$.
故答案为$\frac{25}{4}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了垂径定理和矩形的性质.解决本题的关键是构建直角三角形,利用勾股定理建立关于半径的方程.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:解答题
 在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E.
在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我国青年人喜欢的电视节目应作全面调查 | |
| B. | “购买1张彩票就中奖”是不可能事件 | |
| C. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| D. | 甲、乙两组数据,若${{S}_{甲}}^{2}$>${{S}_{乙}}^{2}$,则乙组数据离散程度大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 随机抛掷一枚硬币,反面一定朝上 | |
| B. | 数据3,3,5,5,8的众数是8 | |
| C. | 某商场抽奖活动获奖的概率为$\frac{1}{50}$,说明毎买50张奖券中一定有一张中奖 | |
| D. | 想要了解长沙市民对“全面二孩”政策的看法,宜采用抽样调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
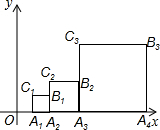 如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com