
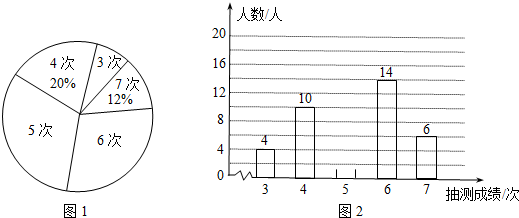
分析 (1)根据4次的有10人,占20%,据此即可求得总人数,然后求得5次的人数,根据众数的定义即可求得众数;
(2)根据(1)的结果即可作出图形;
(3)利用350乘以对应的比例即可求解;
(4)(1)先列举出毎位考生可选择所有方案:50米跑、立定跳远、坐位体前屈(用A表示);50米跑、实心球、坐位体前屈(用B表示);50米跑、立定跳远、1分钟跳绳(用C表示);50米跑、实心球、1分钟跳绳(用D表示);共用4种选择方案.
(2)利用数形图展示所有16种等可能的结果,其中选择两种方案有12种,根据概率的概念计算即可.
解答 解:(1)抽测的总人数是:10÷20%=50(人),
次数是5次的人数是:50-4-10-14-6=16(人),
则众数是:5次;
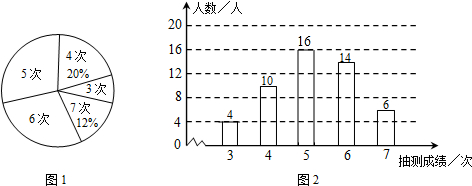
(2)
(3)该校350名九年级男生中估计能达标的人数是:350×$\frac{16+14+6}{50}$=252(人);
(4)(1)
毎位考生可选择:50米跑、立定跳远、坐位体前屈(用A表示);50米跑、实心球、坐位体前屈(用B表示);50米跑、立定跳远、1分钟跳绳(用C表示);50米跑、实心球、1分钟跳绳(用D表示);共用4种选择方案.
故答案为4.
(2)用A、B、C、D代表四种选择方案.(其他表示方法也可)
解法一:用树状图分析如下: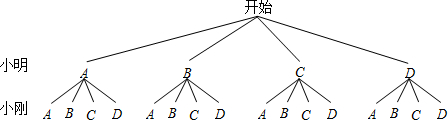
解法二:用列表法分析如下:
| 小刚 小明 | A | B | C | D |
| A | (A,A) | (A,B) | (A,C) | (A,D) |
| B | (B,A) | (B,B) | (B,C) | (B,D) |
| C | (C,A) | (C,B) | (C,C) | (C,D) |
| D | (D,A) | (D,B) | (D,C) | (D,D) |
点评 本题考查的是条形统计图和扇形统计图以及求随机事件概率的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东40°方向航行,乙船沿南偏东50°方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少?
如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东40°方向航行,乙船沿南偏东50°方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
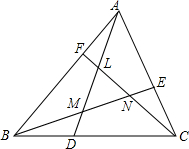 如图,D、E、F分别在△ABC的BC、CA、AB边上,$\frac{BD}{DC}$=$\frac{AF}{FB}$=$\frac{CE}{AE}$=λ,AD、BE、CF交成的三角形为LMN,求S△LMN(用S△ABC表示)
如图,D、E、F分别在△ABC的BC、CA、AB边上,$\frac{BD}{DC}$=$\frac{AF}{FB}$=$\frac{CE}{AE}$=λ,AD、BE、CF交成的三角形为LMN,求S△LMN(用S△ABC表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
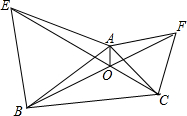 已知△ABC,分别以AB、AC、为边作等边△ABE和等边△ACF,BF与CE交于点O,连接AO,若OA=1,OC=3,OB=4,求线段CE的长.
已知△ABC,分别以AB、AC、为边作等边△ABE和等边△ACF,BF与CE交于点O,连接AO,若OA=1,OC=3,OB=4,求线段CE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com