
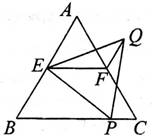
如图,等边△ABC中,点E、F分别是AB、AC的中点,P为BC上一点,连接EP,作等边△EPQ,连接FQ、EF。
(1)若等边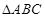 的边长为20,且
的边长为20,且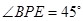 ,求等边
,求等边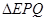 的边长;
的边长;
(2)求证: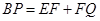 。
。
(1)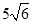 ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)在△BEP中,由条件可知∠B=60°,∠BPE=45°,BE=10,过点E作EM⊥BC于M,通过解直角三角形即可求出EP的长;
(2)取BC边中点N,可证明△ENP≌△EFQ,故NP=FQ.在△ABC中易证△EBN为等边三角形,从而可证BP=EF+FQ.
试题解析:(1)过点E作EM⊥BC于M,
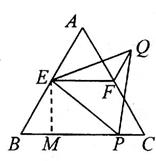
∵等边△ABC
∴∠B=60°
∵E为AB的中点,
∴BE=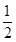 AB=10
AB=10
在Rt△BEM中,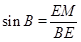
∴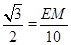
∴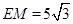
在Rt△EMP中,
∴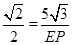
∴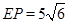 ,即等边△EPQ的边长为
,即等边△EPQ的边长为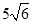
(2)证明:取BC的中点N,连接NE

∵等边△ABC
∴AB=BC
∵E为AB的中点,F为AC的中点,N为BC的中点
∴EF=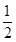 BC,BE=
BC,BE=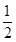 AB,BN=
AB,BN=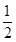 BC,EF∥BC
BC,EF∥BC
∴EF=BE=BN
∵∠B=60°
∴△EBN是等边三角形
∴EN=BN=EF ∠ENB=60°
∵EF∥BC
∴∠FEN=60°
∴∠1+∠2=60°
∵等边△EPQ
∴EP=EQ, ∠PEQ=60°
∴∠2+∠3=60°
∴∠1=∠3
在△ENP和△EFQ中
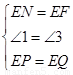
∴△ENP≌△EFQ
∴NP=FQ
∴BP=BN+NP=EF+FQ
考点:1.解直角三角形;2.等边三角形的判定与性质.


科目:初中数学 来源: 题型:
 如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等边△ABC中,D是BC上一点,以AD为边作等腰△ADE,使AD=AE,∠DAE=80°,DE交AC于点F,∠BAD=15°,求∠FDC的度数.
如图,等边△ABC中,D是BC上一点,以AD为边作等腰△ADE,使AD=AE,∠DAE=80°,DE交AC于点F,∠BAD=15°,求∠FDC的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com