
【题目】如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与腰AB相切于点D.
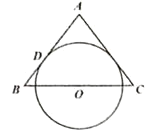
(1)求证:AC与⊙O相切;
(2)已知AB=5,BC=6,求⊙O的半径.
【答案】(1)见解析;(2)![]()
【解析】
(1)连结OD,过点O作OE⊥AC于E点.易证△OBD≌△OCE,从而得OE=OD,从而得证;
(2)连接AO,先利用等腰三角形三线合一的性质得AO⊥BC, OB=![]() BC=3;然后在Rt△AOB中利用勾股定理求出OA,再利用等积关系求出OD即可得解.
BC=3;然后在Rt△AOB中利用勾股定理求出OA,再利用等积关系求出OD即可得解.
解:(1)证明:连结OD,过点O作OE⊥AC于E点,如图1所示:
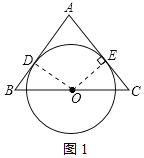
∵AB切⊙O于D,
∴OD⊥AB,
∴∠ODB=∠OEC=90°,
∵O是BC的中点,
∴OB=OC,
∵AB=AC
∴![]()
在△OBD和△OCE中,
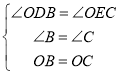 ,
,
∴△OBD≌△OCE(AAS),
∴OE=OD,即OE是⊙O的半径,
∴AC与⊙O相切;
(2)连接AO,如图2所示:
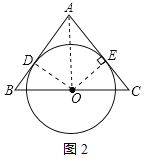
∵OB=OC,AB=AC
则AO⊥BC,
∴OB=![]() BC=3,
BC=3,
∴在Rt△AOB中,OA=![]() =
=![]() =4,
=4,
∴由等积关系得:![]() OBOA=
OBOA=![]() ABOD,
ABOD,
∴OD=![]() =
=![]() =
=![]() ,
,
即⊙D的半径为![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】江苏省第十九届运动会将于2018年9月在扬州举行开幕式,某校为了了解学生“最喜爱的省运会项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表


根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 ,![]() ;
;
(2)扇形统计图中“自行车”对应的扇形的圆心角为 度;
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24 000元购入一批空调,然后以每台3 000元的价格销售,因天气炎热.空调很快售完;商场又用52 000元再次购入一批该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在第二次空调销售中获得的利润率不低于20%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=![]() BC,③OD=
BC,③OD=![]() BF,④∠CHF=45°。正确结论的个数为( )
BF,④∠CHF=45°。正确结论的个数为( )
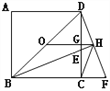
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC的内心为E,连接OE、CE,当点C从点B运动到点A时,内心E所经过的路径长为 ________.
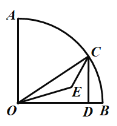
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8,点E是AB的中点,以AE为边作等边△ADE(点D与点C分别在AB异侧),连接CD,则△ACD的面积是_________.
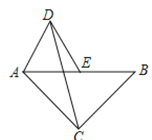
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB与x轴、y轴分别相交于点A、B,将线段AB绕点A顺时针旋转90°,得到AC,连接BC,将△ABC沿射线BA平移,当点C到达x轴时运动停止.设平移距离为m,平移后的图形在x轴下方部分的面积为S,S关于m的函数图象如图2所示(其中0<m≤a,a<m≤b时,函数的解析式不同).
(1)填空:△ABC的面积为 ;
(2)求直线AB的解析式;
(3)求S关于m的解析式,并写出m的取值范围.
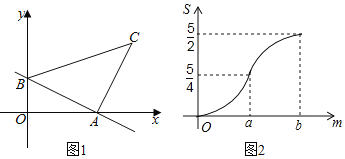
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点![]() (顶点是网格线的交点)和直线l及点O.
(顶点是网格线的交点)和直线l及点O.
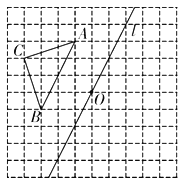
(1)画出![]() 关于直线l对称的
关于直线l对称的![]() ;
;
(2)连接OA,将OA绕点O顺时针旋转![]() ,画出旋转后的线段;
,画出旋转后的线段;
(3)在旋转过程中,当OA与![]() 有交点时,旋转角
有交点时,旋转角![]() 的取值范围为________.
的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
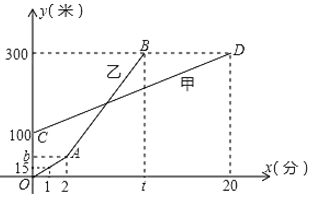
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com