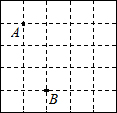
如图.是一个5×5的正方形网格.网格中的每个小正方形的边长均为1．点A和点B在小正方形的顶点上．点C也在小正方形的顶点上．若△ABC为等腰三角形.满足条件的C点的个数为( )A．6B．7C．8D．9 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，是一个5×5的正方形网格，网格中的每个小正方形的边长均为1．点A和点B在小正方形的顶点上．点C也在小正方形的顶点上．若△ABC为等腰三角形，满足条件的C点的个数为（　　）

A．6

B．7

C．8

D．9

分析：分为两种情况：①以AB为腰时，符合条件的有点C D E F G H；②以AB为底时，符合条件的有点I J；相加即可得出答案．

解答：解：

①以AB为腰时，符合条件的有点C D E F G H；
②以AB为底时，符合条件的有点I J；
共6+2=8，
故选C．

点评：本题考查了等腰三角形的判定，注意：有两边相等的三角形是等腰三角形．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

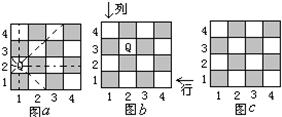39、国际象棋、中国象棋和围棋号称为世界三大棋种．国际象棋中的“皇后”的威力可比中国象棋中的“车”大的多：“皇后”不仅能控制她所在的行与列中的每一个小方格，而且还能控制“斜”方向的两条直线上的每一个小方格．如图a是一个4×4的小方格棋盘，图中的“皇后Q”能控制图中虚线所经过的每一个小方格．
（1）在如图b的小方格棋盘中有一个“皇后Q”，她所在的位置可用“（2，3）”来表示，
则：①“皇后Q”所在的位置“（2，3）”的意义是

第二列，第三行

；
②写出棋盘中不能被该“皇后Q”所控制的四个位置

（1，1），（3，1），（4，2），（4，4）

；
（2）如图c也是一个4×4的小方格棋盘，请在这个棋盘中放入四个“皇后Q”，使这四个“皇后Q”之间互相不受对方控制（在图c中的某四个小方格中标出字母Q即可）．

查看答案和解析>>

科目：初中数学 来源： 题型：

（1）如图1是一个重要公式的几何解释．请你写出这个公式；
（2）如图2，Rt△ABC≌Rt△CDE，∠B=∠D=90°，且B，C，D三点共线．试证明∠ACE=90°；
（3）伽菲尔德（Garfield，1881年任美国第20届总统）利用（1）中的

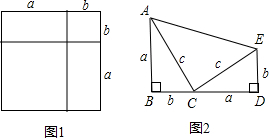公式和图2证明了勾股定理（1876年4月1日，发表在《新英格兰教育日志》上），现请你尝试该证明过程．