
分析 (1)把A(0,3)代入y1和y2中可求得a、b的值;
(2)列方程组,解出即可得出点B的坐标,画图象,根据图象得出当y1≥y2时x 的取值范围;
(3)分别求出两函数s、t的解析式,并配方成顶点式,写出当s 随着x 的增大而增大,且t 也随着x 的增大而增大的x的取值,与n≤x≤m相对应得出结论.
解答  解:(1)把A(0,3)代入y1=x+b中得:b=3,
解:(1)把A(0,3)代入y1=x+b中得:b=3,
∴y1=x+3,y2=a(x2+3x+3),
把A(0,3)代入y2=a(x2+3x+3)中得:3a=3,a=1,
∴a=1,b=3;
(2)由题意得:$\left\{\begin{array}{l}{y=x+3}\\{y={x}^{2}+3x+3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=3}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=1}\end{array}\right.$,
∴B(-2,1),
如图所示,当y1≥y2时x 的取值范围是:-2≤x≤0;
(3)s=y1+y2=x+3+x2+3x+3=x2+4x+6=(x+2)2+2,
∵抛物线开口向上,
∴当x≥-2时,s 随着x 的增大而增大,
t=y1-y2=x+3-(x2+3x+3)=-x2-2x=-(x+1)2+1,
∵抛物线开口向下,
∴当x≤-1时,t随着x 的增大而增大,
∴当-2≤x≤-1时,s 随着x 的增大而增大,且t 也随着x 的增大而增大,
∵n≤x≤m,s 随着x 的增大而增大,且t 也随着x 的增大而增大,
∴n 的最小值-2,m 的最大值-1.
点评 本题考查了利用待定系数法求函数的解析式,明确二次函数的增减性与抛物线的对称轴有关,因此要把二次函数配方成顶点式后写出它的对称轴;本题还利用了数形结合的思想解决了:当y1≥y2时x 的取值范围;此类题有难度,要熟练掌握二次函数的图象的性质.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则△OBD≌△OAC的判定方法是SAS(用字母表示)
如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则△OBD≌△OAC的判定方法是SAS(用字母表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
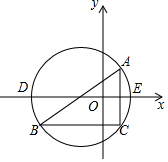 如图,在平面直角坐标系内,已知点A(2,2),B(-6,-4),C(2,-4).
如图,在平面直角坐标系内,已知点A(2,2),B(-6,-4),C(2,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
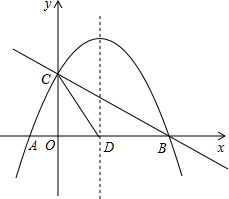 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
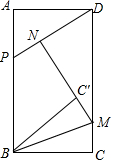 如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点P在线段AB上,满足PB=PD,点M在射线CD上,点C关于直线BM的对称点为点C′,连接C′B、C′M,射线MC′与射线DP交于点N.
如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点P在线段AB上,满足PB=PD,点M在射线CD上,点C关于直线BM的对称点为点C′,连接C′B、C′M,射线MC′与射线DP交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com