Question

6．某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕着直角三角形DBC（DC＜BC）的对角线交点O旋转（如图①→②），图中M、N分别为直角三角板的直角边与三角形DBC的边CD、BC的交点．
（1）我们知道，矩形是轴对称图形，请说出它的对称轴条数和对称轴，根据对称性，试问OA、OB、OC、OD有何数量关系．
（2）该学习小组中一名成员意外地发现：连接DN，发现△BND为特殊的三角形，试问此三角形是何特殊的三角形？并加以说明．
（3）在图①（三角板的一直角边与OD重合）中试问BN、CN、DC的关系并说明理由．
（4）试探究图②中BN、CN、CM、DM这四条线段之间的数量关系，请你用一等式在横线上直接表示出探究的结论：CM²+CN²=DM²+BN²．（不需要说明理由）

Answer 1

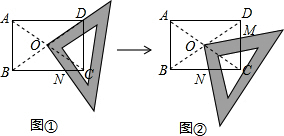
分析 （1）根据矩形的性质即可解决问题．
（2）根据垂直平分线的性质即可解决问题．
（3）作辅助线，连接DN，在Rt△CDN中，根据勾股定理可得：ND²=NC²+CD²，再根据ON垂直平分BD，可得：BN=DN，从而可证：BN²=NC²+CD²．
（4）作辅助线，延长MO交AB于点E，可证：△BEO≌△DMO，NE=NM，在Rt△BEN和Rt△MCN中，根据勾股定理和对应边相等，可证：CN²+CM²=DM²+BN²．

解答 解：（1）结论：OA=OB=OC=OD．
理由：如图①中，∵四边形ABCD是矩形，
∴AO=OC，OB=OD，AC=BD，
∴OA=OB=OC=0D．
（2）结论：△BND为等腰三角形．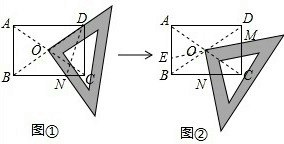
理由：如图①中，∵OB=OD，∠NOD=90°，
∴NO⊥BD，
∴NB=ND，
∴△BDN是等腰三角形．
（3）图①证明：连接DN．
∵四边形ABCD是矩形，
∴BO=DO，∠DCN=90°，
∵ON⊥BD，∴NB=ND，
∵∠DCN=90°，
∴ND²=NC²+CD²，
∴BN²=NC²+CD²．

（2）CM²+CN²=DM²+BN²．
证明：理由如下：
延长MO交AB于E，
∵四边形ABCD是矩形，
∴BO=DO，∠ABC=∠DCB=90°，
∵AB∥CD，∴∠ABO=∠CDO，∠BEO=∠DMO，
∴△BEO≌△DMO，
∴OE=OM，BE=DM，
∵NO⊥EM，
∴NE=NM，
∵∠ABC=∠DCB=90°，
∴NE²=BE²+BN²，NM²=CN²+CM²，
∴CN²+CM²=BE²+BN²，
即CN²+CM²=DM²+BN²．

点评 本题考查了三角形综合题、图形的旋转变化、矩形的性质、勾股定理、全等三角形等知识，解题的关键是这些知识的灵活应用，需要一定的综合能力，属于中考压轴题．