
分析 首先根据方差的计算公式,求出S乙2的值是多少,然后比较出S甲2,S乙2的大小关系,判断出谁的成绩更稳定,即可确定谁去参加比赛,据此解答即可.
解答 解:S乙2=$\frac{1}{10}$[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(7-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2+(7-7)2]
=$\frac{1}{10}$[4+4+0+1+0+1+1+1+0+0]
=$\frac{1}{10}$×12
=1.2
∵1.2<3,
∴S甲2>S乙2,
∴乙的成绩更稳定,所以确定乙去参加比赛.
故答案为:1.2、>、乙、乙.
点评 此题主要考查了方差的含义和性质的应用,要熟练掌握,解答此题的关键是要明确:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
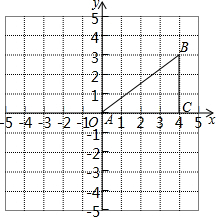 如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.
如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x度时,应交电费为y元.具体收费情况如折线图所示,请根据图象回答下列问题:
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x度时,应交电费为y元.具体收费情况如折线图所示,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com