
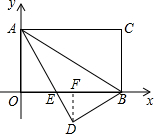
 如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.
如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.分析 (1)根据矩形的性质和轴对称的性质得出OA=BD=4,然后根据AAS证得△AOE≌△BDE,得出AE=BE,OE=ED,设AE=BE=x,则OE=8-x,根据勾股定理列出关于x的方程,解方程求得AE=BE=5,从而求得DE=OE=3,根据三角形面积求得DF,然后根据勾股定理即可求得BF,进而求得OF,得到D的坐标;
(2)根据待定系数法求得即可.
解答 解:(1)∵四边形AOBC是矩形,点C的坐标为(8,4),
∴OA=BC=4,AC=OB=8,
∵AD=AC,BD=BC,
∴AD=8,BD=4,
在△AOE和△BDE中
$\left\{\begin{array}{l}{∠AEO=∠BED}\\{∠AOE=∠BDE=90°}\\{OA=BD}\end{array}\right.$
∴△AOE≌△BDE(AAS),
∴AE=BE,OE=ED,
设AE=BE=x,则OE=8-x,
∵OA2+OE2=AE2,
∴42+(8-x)2=x2,
解得x=5,
∴BE=5,DE=OE=3,
作DF⊥OB于F,
∵$\frac{1}{2}$BD•DE=$\frac{1}{2}$BE•DF,
∴DF=$\frac{BD•DE}{BE}$=$\frac{4×3}{5}$=$\frac{12}{5}$,
∴BF=$\sqrt{B{D}^{2}-D{F}^{2}}$=$\frac{16}{5}$,
∴OF=8-$\frac{16}{5}$=$\frac{24}{5}$,
∴D($\frac{24}{5}$,-$\frac{12}{5}$).
(2)设直线AD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{b=4}\\{\frac{24}{5}k+b=-\frac{12}{5}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=4}\end{array}\right.$,
∴线AD的解析式为y=-$\frac{4}{3}$x+4.
点评 本题考查了矩形的性质,一次函数的图象与几何变换,三角形全等的判定和性质,勾股定理的应用,三角形的面积以及待定系数法求一次函数的解析式.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
 已知抛物线y1=-(x+1)2+4.
已知抛物线y1=-(x+1)2+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
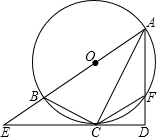 如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC、CF、AC.
如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC、CF、AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
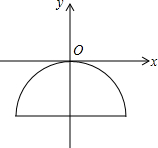 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com