
分析 首先化简已知,进而将已知分式化简,再把已知代入求出答案.
解答 解:由已知可得:x=$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$,
y=$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}$=$\sqrt{3}$+$\sqrt{2}$,
$\frac{{x}^{2}-5xy-6{y}^{2}}{{x}^{2}+xy}$=$\frac{(x-6y)(x+y)}{x(x+y)}$=$\frac{x-6y}{x}$
把x,y的值代入得:
原式=$\frac{x-6y}{x}$
=$\frac{\sqrt{3}-\sqrt{2}-6(\sqrt{3}+\sqrt{2})}{\sqrt{3}-\sqrt{2}}$
=$\frac{-5\sqrt{3}-7\sqrt{2}}{\sqrt{3}-\sqrt{2}}$
=$\frac{(-5\sqrt{3}-7\sqrt{2})(\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}$
=-15-5$\sqrt{6}$-7$\sqrt{6}$-14
=-29-12$\sqrt{6}$.
点评 此题主要考查了二次根式的化简求值,正确化简二次根式是解题关键.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:选择题
| A. | 2017m2017 | B. | 4033m2016 | C. | 4033m2017 | D. | 4034m2017 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
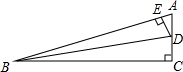 如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.
如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com